|
|
| |
Ciało doskonale czarne to ciało pochłaniające całe padające na nie promieniowanie. Przykładem ciała doskonale czarnego może być ludzkie oko, lub prościej - pudełko z małym otworem. Przez otwór do pudełka wpada promień świetlny i już z niego nie wychodzi, tylko w środku się odbija.
Pudełko jest więc wypełnione promieniowaniem, które jest w równowadze z materią pudełka. To znaczy, że ile promieniowania o danej częstotliwości zostanie przez ścianki pudełka pochłonięte, tyle zostanie w tej samej częstotliwości wyemitowane. I tak jest dla każdej częstotliwości.
Oczywiście pomijamy fakt, że część promieniowania wycieka przez otwór, ale otwór być musi. Po pierwsze, by było którędy wpuścić tam światło, po drugie by można było badać własności promieniowania wypełniającego pudełko. :)
Wyobraźmy sobie teraz kawałek rozgrzanego żelaza (np. u kowala). Przy niższych temperaturach kawałek nie będzie świecić, ale jeśli temperatura osiągnie pewną wartość, zacznie on świecić światłem czerwonym. Im wyższa temperatura, tym kolor jaśniejszy, aż dojdziemy do bieli.
Świecące ciało nie emituje takiej samej energii w każdej długości fali. Jest taka długość fali, dla której wypromieniowana energia osiąga maksimum. Nasze doświadczenie z rozgrzanym żelazem oznacza, że długość fali, dla której mamy maksimum energii promieniowania, zależy od temperatury. Wydaje się, że im wyższa temperatura, tym krótsza długość fali, dla której to maksimum występuje. Dokładniej o tej zależności mówi prawo Wiena wyrażane wzorem:
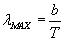
gdzie:
T - temperatura podana w stopniach Kelvina;
b - stała Wiena, mająca wartość
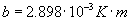
Rzeczywiście im wyższa temperatura, tym dla krótszej fali obserwowane jest maksimum.
Sprawdźmy jeszcze, jak wzrost temperatury wpływa na częstotliwość. Skorzystamy w tym celu z zależności między długością fali a jej częstotliwością
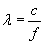
gdzie c to prędkość światła.
Prawo Wiena przyjmuje więc postać:
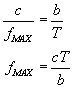
Tak więc im wyższa temperatura, tym większa częstotliwość, dla której jest maksimum.
Całkowita energia emitowana przez jednostkę powierzchni ciała doskonale czarnego w jednostce czasu też zależy tylko od temperatury. Mówi o tym prawo Stefana-Boltzmanna
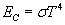
gdzie σ to stała Stefana o wartości
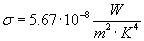
Energia ta jest proporcjonalna do czwartej potęgi temperatury.
Zaraz, zaraz - ktoś mi powie, że jednostką tej wyemitowanej energii jest W/m2, który nigdy nie da dżula! No właśnie, przeczytajcie jeszcze raz prawo Stefana-Boltzmanna - jest tam mowa o jednostce czasu i jednostce powierzchni. Oznacza to, że powyższy wzór domyślnie wyprowadzono dla jednej sekundy i jednego metra kwadratowego i stworzono dla niego nową jednostkę.
Co w przypadku, gdy chcemy uzyskać energię w dżulach, albo mamy daną inną jednostkę czasu lub powierzchni (np. cztery sekundy albo kilometr kwadratowy)? Należy zastosować wzór...
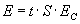
...który wykorzystuje prawo Stefana-Boltzmanna. I wtedy dla każdej wartości powierzchni S i czasu t energia wyjdzie w dżulach.Zobacz też: Zadanie 1 Zadanie 2 Zadanie 3 Zadanie 4 Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
|
|
|
|

|
