|
|
| |
Pojęcie środka masy jest bardzo użyteczne, gdyż jak się przekonamy, pozwala na znakomite uproszczenie opisu ruchu układu składającego się z wielu ciał. Zamiast rozpatrywać poszczególne ruchy dużej ilości ciał, wystarczy w wielu przypadkach rozważyć jedynie ruch jednego punktu będącego środkiem mas układu tych ciał.
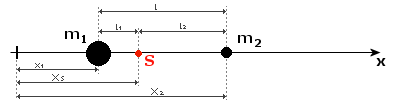
Rozważmy dwa ciała o masach m1 i m2 położone na osi X w punktach x1 i x2 odległe od siebie o l = x2 - x1 (patrz rysunek). Punkt S, który dzieli odcinek l w stosunku odwrotnie proporcjonalnym do mas tych ciał nazywamy środkiem masy układu dwóch ciał (punktów materialnych). Zatem:
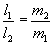
Jeżeli przez xS oznaczymy współrzędną środka masy, to:
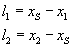
Podstawmy to do naszego powyższego wzoru:
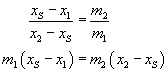
Po nieskomplikowanych przekształceniach otrzymamy wzór na środek masy:
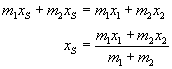
Wzór ten można uogólnić na n punktów materialnych:
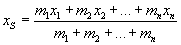
W celu określenia środka masy w przestrzeni należy podać wszystkie trzy współrzędne. Współrzędne yS i zS wyrażają się analogicznymi wzorami do xS.
Środek masy może być w spoczynku lub poruszać się podczas ruchu poszczególnych ciał układu. Zapytajmy, jaka jest prędkość środka masy vS, gdy znane są prędkości i masy ciał układu. Pisząc dwa powyższe równania dla dwóch różnych chwil czasu i odejmując je od siebie stronami, otrzymamy:
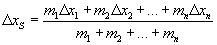
Dzieląc obie strony równania przez Δt = t2 - t1 i uwzględniając, że prędkość środka masy wynosi
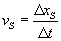oraz że prędkości poszczególnych ciał wynoszą
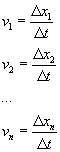otrzymamy:
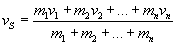
Widzimy, że w liczniku tego wzoru występuje sumaryczny pęd całego układu, a w mianowniku sumaryczna masa całego układu, więc powyższy wzór można zapisać (w postaci wektorowej):
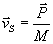
W przypadku, gdy układ jest odosobniony, jego całkowity pęd jest stały i wtedy prędkość środka masy jest również stała co do wartości i co do kierunku, czyli środek masy porusza się ruchem bezwładnym, niezależnie od tego, jak poruszają się części składowe układu. Na układ odosobniony nie działają siły zewnętrzne. Widzimy zatem, że siły wewnętrzne nie wpływają na ruch środka masy.
Jak zachowuje się środek masy, gdy na układ działają siły zewnętrzne? Środek masy uzyskuje wtedy przyspieszenie aS, które można obliczyć z drugiej zasady dynamiki Newtona:
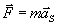
gdzie F oznacza sumę wektorową zewnętrznych sił działających na wszystkie ciała układu. Zatem środek masy układu zachowuje się tak, jak gdyby cała masa układu znajdowała się w punkcie środka masy i jak gdyby wszystkie siły działające na ciała układu były przyłożone do tego punktu.
Na koniec przykład:
Granat spada pionowo w dół. Na pewnej wysokości nad ziemią granat wybucha, odłamki upadają w różne miejsca, ale środek masy wszystkich odłamków spada w dalszym ciągu, tak jakby nic się nie wydarzyło. To znaczy tak, jak gdyby granat spadał nie rozrywając się na części. Dzieje się tak dlatego, gdyż granat rozpada się tylko pod wpływem sił wewnętrznych, które w czasie wybuchu działają na odłamki granatu, a siły wewnętrzne nie wpływają na ruch środka masy układu.Zobacz też: Druga zasada dynamiki Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
|
|
|
|
|
