Na poniższych trzech rysunkach przedstawiliśmy wychylenie x jako funkcję czasu t dla różnych prostych ruchów harmonicznych.
Rysunek 1
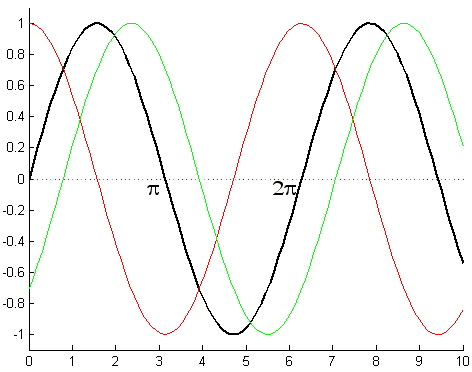
Na rysunku tym wykresy mają jednakowe amplitudy A i okresy T.
Przyjąłem, że:
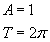Jednakże każdy z wykresów ma inne fazy początkowe:
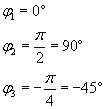gdzie indeksy oznaczają kolejno wykres czarny, czerwony i zielony. Wykres czarny przyjęliśmy jako punkt odniesienia dla pozostałych wykresów (dlatego jego faza jest równa zeru).
Zauważ jeszcze, że
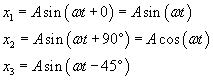
Rysunek 2
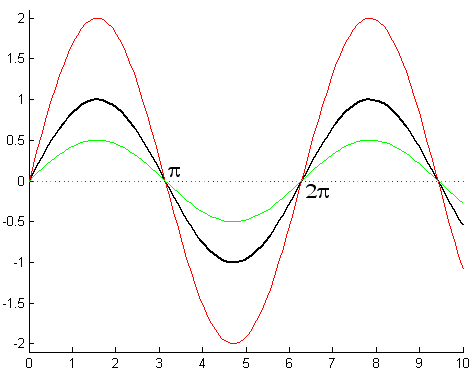
Teraz wszystkie wykresy mają jednakową fazę początkową φ oraz okresy T.
Przyjąłem, że:
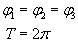gdzie indeksy oznaczają kolejno wykres czarny, czerwony i zielony.
Każdy z wykresów ma jednak różne amplitudy, i tak:
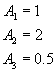Stąd:
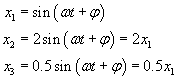
Rysunek 3
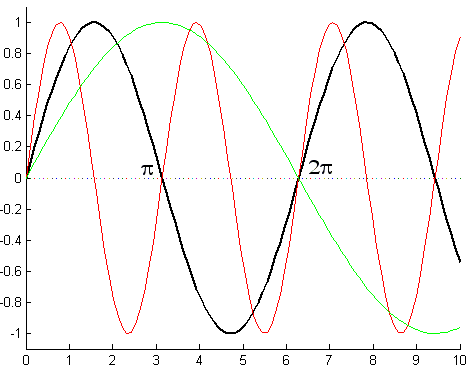
Każdy z wykresów ma jednakową amplitudę oraz fazę początkową (np. równą zeru).
Przyjąłem, że:
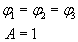gdzie indeksy kolejno oznaczają wykres czarny, czerwony i zielony.
Każdy z wykresów ma jednak różne okresy:
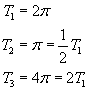Korzystając ze wzoru na okres w ruchu harmonicznym prostym...
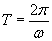...wyliczymy wartości ω dla poszczególnych wykresów:
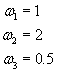Stąd:
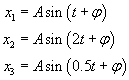« powrót do listy doświadczeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
