W rozważaniach teoretycznych zauważyliśmy, że energia potencjalna i energia kinetyczna wynoszą kolejno
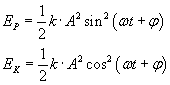gdzie:
k - stała sprężystości,
A - amplituda (maksymalne wychylenie),
ωt + φ - faza.
Ponieważ funkcje sinus i cosinus przyjmują wartości od -1 do 1, to energie maksymalne wynoszą odpowiednio:
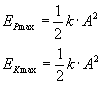przy czym energia potencjalna jest maksymalna w punkcie maksymalnego wychylenia (amplituda), a energia kinetyczna w położeniu równowagi.
Narysujmy wykres zależności energii potencjalnej i energii kinetycznej od czasu. W chwili t = 0 ciało znajdowało się w stanie równowagi.
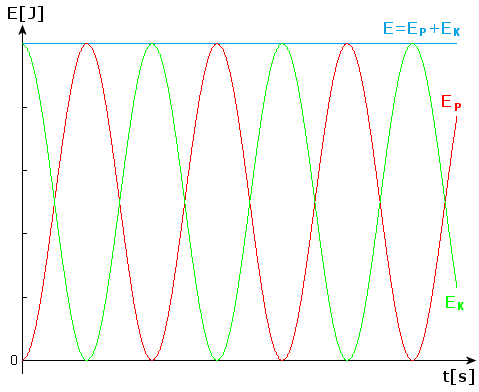Widzimy, że suma energii potencjalnej i kinetycznej jest stała zgodnie z zasadą zachowania energii.
Narysujmy jeszcze wykres zależności energii od wychylenia względem położenia równowagi. Pamiętajmy, że
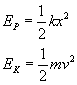Jak to narysować? Trzeba narysować parabolę dla energii potencjalnej. Wiedząc, że różnica energii mechanicznej i energii potencjalnej daje energię kinetyczną, dorysowujemy drugą parabolę.
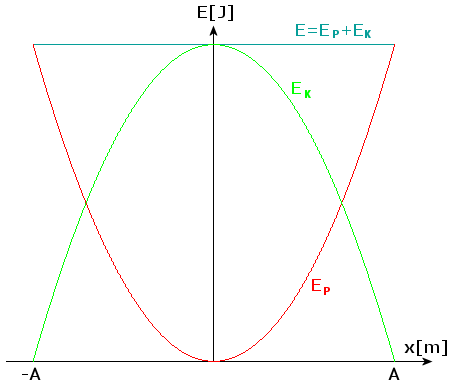Widzimy, że całkowita energia mechaniczna jest stała, jak tego oczekiwaliśmy, a jej wartość wynosi
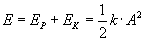Przy maksymalnym wychyleniu (x = A) energia kinetyczna równa się zeru, a energia potencjalna osiąga maksimum EPmax.
Natomiast w położeniu równowagi (x = 0) energia potencjalna równa się zeru, a pozostaje tylko energia kinetyczna o wartości EKmax.
Przy pośrednich położeniach energia kinetyczna i energia potencjalna zmieniają się tak, że ich suma zawsze jest równa 0.5.kA2.« powrót do listy doświadczeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
