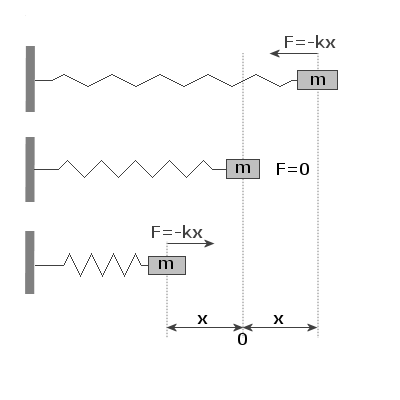
|
|
| |
Na powyższym rysunku przedstawiony jest prosty oscylator harmoniczny. Jest nim klocek o masie m przyczepiony do sprężyny o stałej sprężystości k. Pierwsza sprężyna jest rozciągnięta, druga jest w stanie równowagi, a trzecia jest ściśnięta. W każdym z trzech przypadków przedstawiona jest siła F, z jaką sprężyna działa na masę m. Zakładamy, że klocek ślizga się po doskonale gładkim poziomym stole.
Zwróć uwagę, że istnieje położenie (położenie równowagi), w którym sprężyna nie działa żadną siłą na ciało. Jeżeli ciało jest przesunięte w prawo, to sprężyna oddziałuje na ciało siłą skierowaną w lewo, wynoszącą F = -kx. Jeżeli ciało jest przesunięte w lewo, to siła działa na prawo i wynosi także F = -kx. W tym przypadku jest to siła przywracająca równowagę układowi. Ruch drgającego klocka jest ruchem harmonicznym prostym. Ruch harmoniczny prosty charakteryzuje się również tym, że granice wychyleń są jednakowe po obu stronach położenia równowagi (u nas jest to wartość x).
Stosując drugą zasadę dynamiki Newtona (F = ma), otrzymamy równanie:
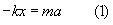
I tutaj zaczynają się schody. student politechniki zapisałby powyższe równanie jako...
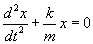
...po czym by stwierdził, że jest to proste tzw. równanie różniczkowe i znalazłby wartość x.
Dla ucznia / uczennicy szkoły średniej jest to zbyt trudne, dlatego bez wyliczania podaje się rozwiązanie równania (1), które należy zapamiętać
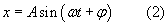gdzie:
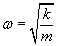
Kosmos? Spokojnie, spróbujemy to wyjaśnić. :)
Najpierw omówimy fizyczne znaczenie stałej ω. Jeżeli w równaniu (2) zwiększymy czas t o 2π/ω, to funkcja x przyjmie postać:
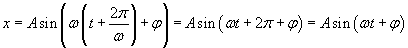
Widzimy, że po czasie 2π/ω funkcja ta przyjmuje swoją poprzednią wartość. Zatem 2π/ω jest okresem T ruchu harmonicznego prostego.
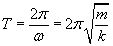
Stała A ma proste znaczenie fizyczne. Funkcja sinus przyjmuje wartości od -1 do 1. Wychylenie x z położenia równowagi osiąga wartość maksymalną równą właśnie stałej A. Zatem:
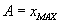
Stałą A nazywamy amplitudą ruchu. Czyli amplituda to inaczej wychylenie maksymalne (równe na naszym rysunku wartości x).
Wielkość (ωt+φ) nazywamy fazą ruchu, przy czym φ jest fazą początkową.
Dwa ruchy mogą mieć te same amplitudy i częstości, lecz różne fazy. Jeżeli np. φ=-π/2, to:
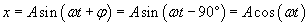
czyli przemieszczenie jest maksymalne w chwili t = 0. Jeżeli φ = 0, to przemieszczenie x = Asin(ωt) jest zerowe w chwili t = 0.
Amplituda A i faza początkowa φ drgań zależą od początkowego położenia i prędkości punktu materialnego.
Aby uzmysłowić te rozważania proponuję przeanalizować temat "Amplituda, okres, faza", do którego link znajduje się poniżej oraz po prawo w sekcji "Zobacz też".
Zdefiniujemy jeszcze prędkość (pierwsza pochodna z wychylenia po czasie) oraz przyspieszenie (druga pochodna) drgającego punktu materialnego.
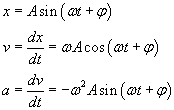
Wartości maksymalne przemieszczenia, prędkości i przyspieszenia mają wartość
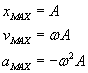
Przy maksymalnym wychyleniu w obydwu kierunkach prędkość równa jest zeru, ponieważ musi wtedy zmieniać kierunek. Przyspieszenie w takiej chwili, podobnie jak siła przywracająca równowagę, osiąga wartość maksymalną, lecz jest skierowane przeciwnie do przemieszczenia. Kiedy wychylenie jest zerowe, prędkość punktu materialnego osiąga maksimum, a przyspieszenie znika, tak jak to się dzieje z siłą przywracającą równowagę. Prędkość wzrasta w miarę zbliżania się punktu materialnego do położenia równowagi i maleje w miarę zbliżania się do maksymalnego wychylenia.Zobacz też: Amplituda, okres, faza Prędkość w ruchu drgającym II zasada dynamiki Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
|
|
|
|
|
