W ruchu harmonicznym prostym o wychyleniu
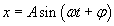
w którym nie występują żadne siły rozpraszające (np. tarcie), całkowita energia mechaniczna jest zachowana (pozostaje stała). Całkowita energia to suma energii potencjalnej i kinetycznej.
A. Energia potencjalna
Ciało drgające ruchem harmonicznym prostym posiada energię potencjalną wtedy, gdy znajduje się ono w jakimś wychyleniu od stanu równowagi. Gdy ciało znajduje się więc w położeniu równowagi, nie posiada energii potencjalnej.
Energia potencjalna jest równa energii potencjalnej sprężystości, którą możemy wyrazić wzorem:
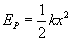
Uwzględniając wzór na wychylenie x, otrzymujemy:
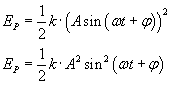
Maksymalna wartość energii potencjalnej wynosi
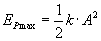
i ciało ma tę energię wtedy, gdy znajduje się w położeniu maksymalnego wychylenia (amplitudy).
B. Energia kinetyczna
Ciało o masie m drgające ruchem harmonicznym prostym posiada energię kinetyczną wtedy, gdy posiada ono jakąś prędkość v w danej chwili. Oznacza to, że ciało nie posiada energii kinetycznej wtedy, gdy prędkość równa jest zeru, a taki moment następuje, gdy ciało znajduje się w położeniu maksymalnego wychylenia (x = A).
Energię kinetyczną wyrażamy wzorem:
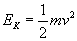
Ponieważ w ruchu harmonicznym:
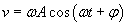to:
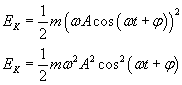
Przypominam, że
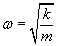stąd:
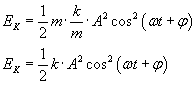
Maksymalna wartość energii kinetycznej wynosi
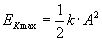
i mamy z nią do czynienia, gdy drgające ciało ma największą prędkość (a jak wiemy, ma ono ją wtedy, gdy znajduje się w punkcie równowagi x = 0).
C. Energia mechaniczna
Przypominam, że energia mechaniczna w danym momencie jest równa:
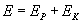Stąd biorąc powyższe:
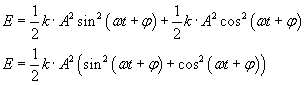
Korzystając z zależności trygonometrycznej
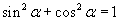mamy ostatecznie:
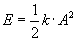
Całkowita energia punktu materialnego poruszającego się ruchem harmonicznym prostym jest proporcjonalna do kwadratu amplitudy tego ruchu.
Zobacz też: Energia w ruchu drgającym - wykresy Prędkość w ruchu drgającym Zasada zachowania energii Energia kinetyczna Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
