Spójrzmy na punkt trzeci naszego rozdziału. Piszę tam, że ruch jednostajny po okręgu to taki ruch, w którym wartość prędkości liniowej jest stała. No dobrze - ale z drugiego rozdziału wszyscy wiemy (mam nadzieję), że jeśli prędkość jest stała, to nie ma przyspieszenia...
A jednak w tym rodzaju ruchu jest. Spróbujmy rozważyć ten problem.
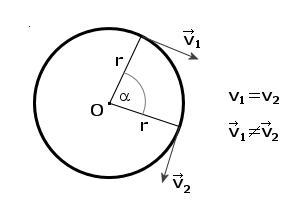Pamiętacie ten obrazek? Tak, był on też w punkcie drugim. Spójrzmy na dwa zapisy prędkości obok rysunku. Prędkości te mają jednakowe wartości liczbowe, ale RÓŻNE kierunki. Oczywiście dlatego te wektory są różne. Jeśli wektory prędkości v1 i v2 nie są sobie równe, to ich różnica, czyli przyrost prędkości Δv jest różny od zera i wobec tego istnieje przyspieszenie wyrażane wzorem:
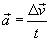
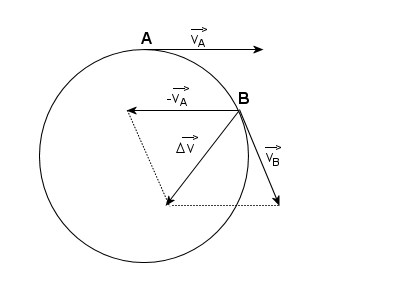Z rysunku widać, że wektor Δv jest równy:
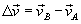
Przyspieszenie to nazywamy dośrodkowym, bo kierunek wektora przyrostu prędkości Δv, a tym samym przyspieszenie, dąży do kierunku promienia, zwrot zaś jest ku środkowi okręgu (lepiej to widać dla mniejszych odległości punktów, z których wychodzą wektory v1 i v2).
Na koniec podam wzór na przyspieszenie dośrodkowe (dokładne wyprowadzenie tego wzoru znajdziesz w dziale Wyprowadzenia):
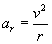
I na koniec zgrabnie to wszystko podsumujmy:
1. wektor prędkości liniowej jest styczny do okręgu, a wektor przyspieszenia dośrodkowego jest zwrócony ku środkowi okręgu. Jest więc prostopadły do wektora prędkości liniowej,
2. przyspieszenie jest konsekwencją zmiany kierunku prędkości, a nie zmiany wartości prędkości.Zobacz też: Przyspieszenie Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
