Aby sformu³owaæ zasadê zachowania energii musimy dowiedzieæ siê, co to s± si³y zachowawcze. Przyk³adem si³y zachowawczej jest si³a grawitacji. Je¿eli podniesiemy cia³o na pewn± wysoko¶æ, to praca wykonana przez si³ê równ± sile ciê¿ko¶ci, lecz przeciwnie skierowan± nie ginie, ale odnajdujemy j± w energii potencjalnej, któr± mo¿emy znów wykorzystaæ do wykonania pracy. Mówimy, ¿e praca wykonana przeciwko sile ciê¿ko¶ci zosta³a "zachowana". Tarcie natomiast nale¿y do si³ niezachowawczych. Zwi±zane jest to z tym, ¿e przy dzia³aniu si³y tarcia wydziela siê ciep³o i energia siê rozprasza. Nie mo¿na jej odzyskaæ w prosty sposób.
Energia mechaniczna cia³a to suma energii potencjalnej i kinetycznej danego cia³a.
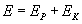
Zasada zachowania energii odnosi siê do uk³adów zachowawczych, czyli takich, w których dzia³aj± tylko si³y zachowawcze.
We¼my pod uwagê cia³o o masie m spadaj±ce w pró¿ni z wysoko¶ci h. Gdyby¶my przebadali dok³adnie ruch cia³a na wszystkich etapach spadania, obliczaj±c energiê potencjaln± i energiê kinetyczn±, to stwierdziliby¶my, ¿e suma tych energii pozostaje w ka¿dym momencie wielko¶ci± sta³±.
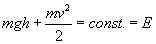Wielko¶æ E zwana ca³kowit± energi± mechaniczn± uk³adu jest zachowana. Natomiast dwa sk³adniki tej energii doznaj± w ci±gu ruchu zmian, przechodz±cych wzajemnie w siebie. Gdy cia³o znajduje siê na wyskoko¶ci h, energia ca³kowita równa siê energii potencjalnej. W nastêpnych momentach, gdy ruch siê zacznie i cia³o zmniejsza swoj± wysoko¶æ, maleæ bêdzie energia potencjalna, a odpowiednio narastaæ energia kinetyczna. Na koñcu ruchu, gdy h = 0 energi± ca³kowit± bêdzie energia kinetyczna.
Zasadê zachowania energii mo¿emy wiêc wypowiedzieæ:
Suma energii kinetycznej i potencjalnej w uk³adzie, na który nie dzia³aj± si³y zewnêtrzne i nie nastêpuje w nim rozpraszanie energii wskutek dzia³ania si³ niezachowawczych, jest wielko¶ci± sta³±.
Zobacz te¿: Zadanie 18 Znalaz³e¶ b³±d w materiale? Skontaktuj siê z nami, przysy³aj±c adres strony, na której znajduje siê b³±d i informacjê o tym, czego dotyczy b³±d.
