 Na ciało o masie m działają następujące siły:
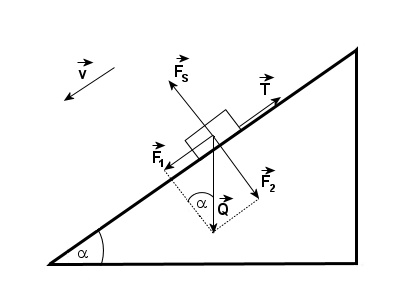
Na ciało o masie m działają następujące siły:
- siła przyciągania ziemskiego Q skierowana pionowo do dołu,
- siła tarcia T równoległa do powierzchni równi,
- siła sprężystości podłoża FS prostopadła do powierzchni równi.
Każda z tych sił ma inny kierunek.Wyznaczamy składowe wektora siły przyciągania ziemskiego Q = mg:
- równoległą do powierzchni równi F1:
 - prostopadłą do powierzchni równi F2:
- prostopadłą do powierzchni równi F2:
 Siły działające prostopadle do równi równoważą się:
Siły działające prostopadle do równi równoważą się:
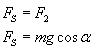 Siła sprężystości jest siłą reakcji na nacisk ciała na powierzchnię równi. Zatem zgodnie z III zasadą dynamiki:
Siła sprężystości jest siłą reakcji na nacisk ciała na powierzchnię równi. Zatem zgodnie z III zasadą dynamiki:
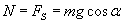 Największy nacisk wywiera ciało znajdujące się na poziomym torze, ponieważ cos 0o = 1 i wtedy:
Największy nacisk wywiera ciało znajdujące się na poziomym torze, ponieważ cos 0o = 1 i wtedy:
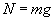 Rozpatrzmy teraz trzy różne przypadki.
Rozpatrzmy teraz trzy różne przypadki.
Przypadek 1 - ciało pozostaje w spoczynku na równi pochyłej
Ciało pozostaje w spoczynku wtedy, gdy działające na nie siły równoważą się.
W tym przypadku siłę F1 równoważy siła tarcia statycznego TS:
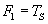 Siła tarcia statycznego nie może przekroczyć wartości (patrz: Teoria - Tarcie):
Siła tarcia statycznego nie może przekroczyć wartości (patrz: Teoria - Tarcie):
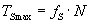 Zatem:
Zatem:
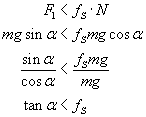 Otrzymaliśmy warunek, jaki musi spełniać kąt α, aby ciało pozostawało na równi w spoczynku (gdzie fS - współczynnik tarcia statycznego).
Otrzymaliśmy warunek, jaki musi spełniać kąt α, aby ciało pozostawało na równi w spoczynku (gdzie fS - współczynnik tarcia statycznego).
Przypadek 2 - ciało zsuwa się z równi pochyłej
Podczas zsuwania się ciała z równi siła tarcia dynamicznego T jest skierowana przeciwnie do siły F1 i ma wartość:
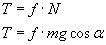 Siła wypadkowa w tym przypadku ma wartość:
Siła wypadkowa w tym przypadku ma wartość:
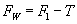 Jeżeli F1 = T, to ciało zsuwa się z równi ruchem jednostajnym (I zasada dynamiki).
Jeżeli F1 > T, to ciało zsuwa się ruchem jednostajnie przyspieszonym z przyspieszeniem (II zasada dynamiki):
Jeżeli F1 = T, to ciało zsuwa się z równi ruchem jednostajnym (I zasada dynamiki).
Jeżeli F1 > T, to ciało zsuwa się ruchem jednostajnie przyspieszonym z przyspieszeniem (II zasada dynamiki):
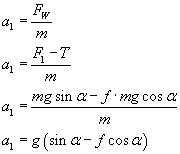 Jeżeli równia jest idealnie gładka, czyli f = 0, to przyspieszenie jest wprost proporcjonalne do sinusa kąta nachylenia równi:
Jeżeli równia jest idealnie gładka, czyli f = 0, to przyspieszenie jest wprost proporcjonalne do sinusa kąta nachylenia równi:
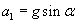
Przypadek 3 - ciało posuwa się w górę równi pochyłej
Ciału nadano prędkość skierowaną pod górę równi. Podczas ruchu pod górę zarówno siła tarcia T, jak i siła F1, działają przeciwnie do ruchu ciała. Ciało takie porusza się ruchem jednostajnie opóźnionym (II zasada dynamiki) aż do zatrzymania.
Siła wypadkowa wynosi:
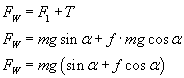 Zatem możemy wyliczyć opóźnienie:
Zatem możemy wyliczyć opóźnienie:
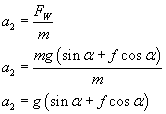 I analogicznie - jeśli f = 0:
I analogicznie - jeśli f = 0:
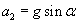
Wnioski:
Przy ruchu po równi pochyłej idealnie gładkiej (f = 0) czas wznoszenia równy jest czasowi zsuwania:
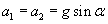 Natomiast gdy f > 0, czas wznoszenia jest krótszy od czasu zsuwania:
Natomiast gdy f > 0, czas wznoszenia jest krótszy od czasu zsuwania:
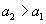 « powrót do listy wyprowadzeń
« powrót do listy wyprowadzeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
