Mamy ciało drgające ruchem harmonicznym prostym o wychyleniu
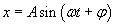W dziale "Teoria" wyprowadziliśmy wzór na prędkość korzystając z tego, że jest ona pierwszą pochodną wychylenia po czasie
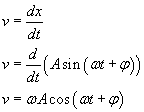Spróbujemy znaleźć wzór na prędkość korzystając z przemian energetycznych zachodzących w tym ruchu. Wiemy bowiem, że energia potencjalna i energia kinetyczna są równe
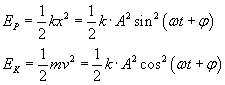Energia mechaniczna to suma energii potencjalnej i energii kinetycznej i jest ona zawsze stała w każdej chwili czasu:
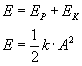Zauważ, że możemy również zapisać:
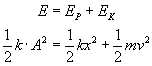Wyprowadzamy z tej równości wzór na prędkość
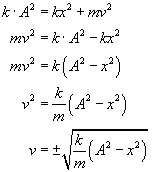Uwzględniając to, że...
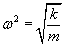otrzymamy...
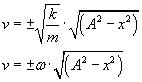Teraz widać wyraźnie, że maksimum prędkości przypada w położeniu równowagi x = 0, a wartość zerowa przy wychyleniu maksymalnym x = A.
Uwaga!
Po scałkowaniu naszego wyniku otrzymamy przemieszczenie jako funkcję czasu, czyli
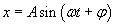« powrót do listy wyprowadzeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
