Pierwszy satelita krąży wokół Ziemi po orbicie kołowej o promieniu r1. Drugi satelita również krąży wokół Ziemi po orbcie kołowej o promieniu r2=3r1. Ile wynosi stosunek ich mas, jeżeli ich energie całkowite są równe?
|
Energia całkowita E satelity jest sumą jego energii kinetycznej i energii potencjalnej
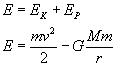Ponieważ w zadaniu nie mamy nic powiedziane o prędkościach satelitów, spróbujmy tę prędkość jakoś inaczej wyrazić.
Wiemy, że satelity poruszają się po orbitach kołowych, działa więc na nie siła dośrodkowa, która wypycha satelitę z toru. Ale ponieważ satelita nie ucieka nam z orbity, siłę tę musi więc równoważyć siła przyciągania satelity do planety, czyli siła grawitacji. Zgodnie z pierwszą zasadą dynamiki siły te muszą być sobie równe - to gwarantuje, że satelita nie zmieni toru swojego ruchu, tak więc:
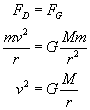Pamiętaj, że m to masa satelity, M - masa Ziemi, a r to odległość satelity od środka Ziemi.
Podstawiamy naszą prędkość do naszych wcześniejszych wyliczeń dotyczących energii
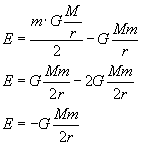Pora skorzystać z tego wzoru i zapisać energię całkowitą dla obu satelitów:
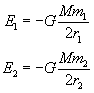Oczywiście stała grawitacji G i masa Ziemi M dla obu przypadków nie zmienią się. Ponieważ E = const, to:
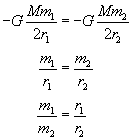Podstawiamy nasze dane i wyliczamy szukany stosunek mas.
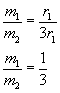
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
