Jakie jest przyspieszenie grawitacyjne na planecie, której zarówno promień, jak i masa, są dwa razy większe od promienia i masy Ziemi?
|
RZ - promień Ziemi
MZ - masa Ziemi
RP = 2RZ - promień planety
MP = 2MZ - masa planety
gZ - przyspieszenie grawitacyjne Ziemi
G - stała grawitacji
gP = ?
1. Prawo powszechnego ciążenia:
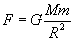
2. Siła ciężkości (grawitacji):
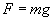
|
|
|
Napiszmy wzór na prawo powszechnego ciążenia dla Ziemi:
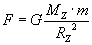
gdzie:
m - masa jakiegoś ciała znajdującego się na powierzchni Ziemi.
Wiemy również, że na powierzchni Ziemi na ciało o masie m działa siła grawitacji wyrażana wzorem:
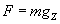
Przyrównajmy dwa powyższe wzory...
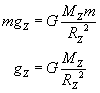
Zauważmy, że wzór na przyspieszenie grawitacyjne jakiejkolwiek planety zależy tylko od masy i promienia tej planety (stała G jest zawsze taka sama). Możemy więc napisać wzór na przyspieszenie grawitacyjne dla naszej szukanej planety:
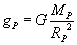
Z treści zadania wiemy, że RP = 2RZ i że MP = 2MZ. Wykorzystajmy te dane, podstawiając je do powyższego wzoru:
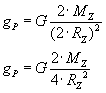
I teraz najważniejsza rzecz w tym zadaniu. Liczymy dalej:
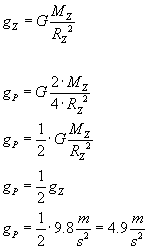
Napisałem tu dwa wzory na przyspieszenie grawitacyjne. Pierwszy dla Ziemi, drugi dla szukanej planety. Zauważmy, że w drugim wzorze, gdy wyciagniemy na początek wszystkie wartości liczbowe, zostanie nam wyrażenie przedstawiające przyspieszenie grawitacyjne Ziemi. Dlatego w to miejsce możemy wstawić gZ i... po zadaniu. :)Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
