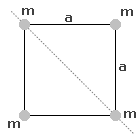
 Cztery jednakowe kulki, każda o masie m, połączono czterema nieważkimi prętami tak, że znajdują się w wierzchołkach kwadratu o boku a. Ile wynosi moment bezwładności otrzymanego układu względem osi obrotu (przerywana linia)? Kulki traktujemy jako punkty materialne.
|
n = 4;
m - masa każdej z kulek A, B, C i D;
a - długość pręta, z którego wykonano bok kwadratu
I = ?
1. Moment bezwładności układu:
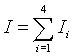
2. Moment bezwładności punktu materialnego:
|
|
|
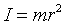
Rozwiązanie tego zadania polega na przekształceniu wzoru na całkowity moment bezwladności układu,
a więc do dzieła :)
Moment bezwładności bryły to suma momentów bezwładności wszystkich punktów tej bryły,
czyli dla kwadratu:
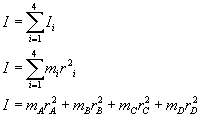
Moment bezwładności jednego punktu bryły, to iloczyn jego masy i odległości od osi obrotu.
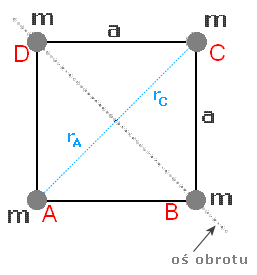
Teraz zauważmy, że przekątna kwadratu ma długość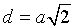 
a odległość punktów A i C
od osi obrotu to połowa długości tej przekątnej czyli:
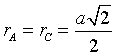
Widzimy też, że punkty B i D leżą na osi obrotu, czyli: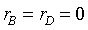 
Teraz wstawiamy wartości tych promieni do naszego wzoru:
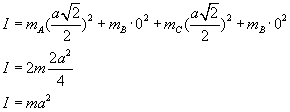
A więc moment bezwładności wynosi: I=ma2.namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
