Koło zamachowe w kształcie pierścienia o promieniu r=0.3m i masie m=50kg obraca się z częstością n=20s-1. Ile musi wynosić moment siły hamującej, aby koło zatrzymało się w czasie t=20s?
|
Rozwiązanie tego zadania opiera się w 100% na skorzystaniu z II zasady dynamiki Newtona dla ruchu obrotowego i przepisaniu jej matematycznej formuły z uwzględnienie odpowiednich zależności. A więc do dzieła.
Wspomniana zasada ma następującą postać:
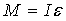
Uwzględniając, że:
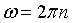
oraz
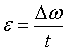
i
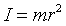
możemy to równanie przepisać w następujący sposób:
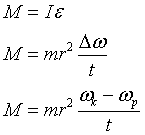
Ponieważ my chcemy, aby koło zamachowe się zatrzymało, więc jego końcowa prędkość kątowa ωk=0.Przekształćmy dalej nasze równanie
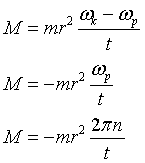
Minus w ostatnim równaniu oznacza, że wektory prędkości kątowej i momentu siły hamującej mają przeciwne zwroty. Ponieważ mamy policzyć wartość momentu siły, przeto pominiemy w dalszych obliczeniach ten znak, pamiętając jednak co on oznacza. Teraz wystarczy tylko zwymiarować nasze równanie i podstawić wartości liczbowe.
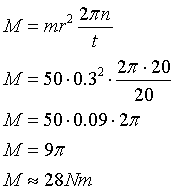
Na koniec sprawdzimy poprawność jednostki:
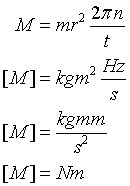
Moment siły hamującej jest równy M = 28 Nmnamysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
