Walec o masie m, promieniu r i momencie bezwładności (1/2)mr2 stacza się bez poślizgu z równi pochyłej o wysokości h. Jaką prędkość osiągnie ten walec u podstawy równi?
|
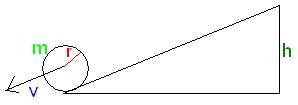Aby policzyć prędkość walca przy podstawie równi pochyłej skorzystamy z najważniejszego prawa w mechanice, czyli zasady zachowania energii. Na szczycie równi prędkość jest zerowa, czyli energia kinetyczna tez jest równa 0, natomiast energia potencjalna jest wtedy maksymalna, ponieważ przyjmujemy, że przy podstawie równi jest równa 0 (założenie to nie jest konieczne, ale ułatwi nam zapis).
Pamiętajmy również, że walec się toczy, tak więc musimy uwzględnić energię kinetyczną ruchu obrotowego (ale tylko u podstawy równi, ponieważ na jej szczycie walec się nie toczy).
Ponieważ całkowita energia mechaniczna ma się nie zmieniać podczas staczania się walca, więc energia potencjalna całkowicie przekształci się w energię kinetyczną ruchu obrotowego i postępowego. Zasada zachowania energii przyjmuje postać:
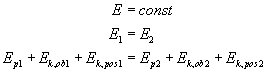
Wielkości z indeksem 1 to wartości na górze równi, a z indeksem 2 u jej podstawy.
Uwzględniając nasze założenia co do wartości energii w tych miejscach możemy napisać:
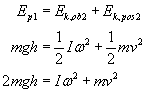
Teraz wykorzystując zależność między prędkością kątową i liniową możemy przepisać nasze równanie w następujący sposób:
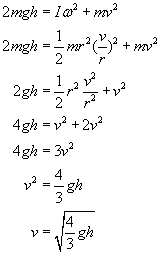
namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
