Bryła sztywna wiruje wokół stałej osi i względem tej osi ma moment pędu L oraz moment bezwładności I. Ile wynosi okres obrotu bryły względem tej osi?
|
Pamiętajmy, że okres to czas pełnego obrotu, czyli możemy napisać:
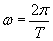
Ponieważ w zadaniu mamy dany moment pędu, musimy skorzystać również ze wzoru nr 3), który jest zapisany w postaci wektorowej. Ponieważ szukamy sposobu na wyrażenie wartości okresu, zamieniamy wzór z postaci wektorowej na postać skalarną:
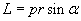
gdzie sinα to kąt między wektorami pędu p i odległości (promienia) r.
Teraz zauważmy, że wektory pędu i promienia w ruchu obrotowym są prostopadłe, a więc sinα=1. Możemy więc napisać:
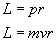
(tak naprawdę wystarczy, że zapamiętasz, że moment pędu w ruchu obrotowym to iloczyn masy, prędkości i odległości).
Teraz uwzględniając zależność między prędkością liniową i kątową możemy powyższe równanie przepisać w następujący sposób:
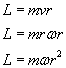
Ze wzoru na moment bezwładności wyznaczymy kwadrat promienia
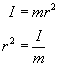
Teraz powyższy wzór i wzór nr 1) wstawimy do przekształconego wzoru na moment pędu

Tak więc okres wyrażamy wzorem
T=(2πI)/L.namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
