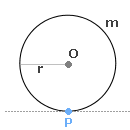
 Ile wynosi moment bezwładności cienkiej, jednorodnej obręczy o masie m i promieniu r względem osi prostopadłej do płaszczyzny wyznaczonej przez obręcz i przechodzącej przez punkt P leżący na obręczy (przerywana linia na rysunku)?
|
m - masa obręczy
r - promień obręczy
I=?
Moment bezwładności obręczy względem osi prostopadłej do płaszczyzny rysunku i przechodzącej przez punkt O
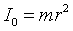
Twierdzenie Steinera
|
|
|
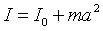
Rozwiązanie tego zadania ogranicza się do skorzystania z twierdzenia Steinera. Oznaczmy długość odcinka OP przez a, aby można było z tego twierdzenia skorzystać.
Zauważmy ponadto, że a=r. No to do dzieła :)
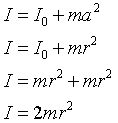
(DLA DOCIEKLIWYCH)
Wyprowadzimy więc sobie wzór na I0.
Wiemy, że moment bezwładności dowolnej bryły to suma momentów bezwładności wszystkich punktów wchodzących w skład bryły względem danej osi obrotu, co ilustruje wzór:
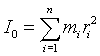
Mamy mały problem, ponieważ obręcz składa się z nieskończenie wielu punktów.
Dokonamy tego poprzez całkowanie. Podzielmy (w ramach eksperymentu myślowego) obręcz na na nieskończenie małe elementy o długości dx. Oznaczmy elementy bezwładności każdego z tych elementów przez dI. Wprowadźmy sobie gęstość liniową jako stosunek masy do długości. W naszym przypadku:
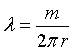
Gdzie λ to właśnie gęstość liniowa.
Element dx naszej obręczy możemy traktować jako punkt, a więc jego moment bezwładności wyraża wzór:
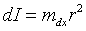
Przez mdx oznaczyłem masę tego elementu tarczy.
Ale zauważmy, że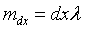 
Więc nasze równanie przyjmuje postać 
Teraz obustronnie scałkujemy to równanie i trochę przekształcimy
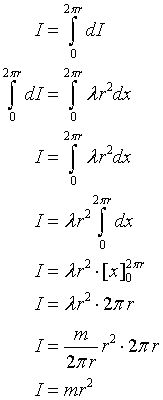
A więc słusznie zastosowaliśmy taki, a nie inny wzór na moment bezwładności obręczy :)
Szukany moment bezwładności wynosi I=2mr2.namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
