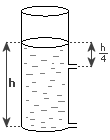
|
|
|
 |
|
|
|
|
|
|
| |
 W naczyniu o kształcie walca, w którym zrobiono dwa otworki, znajduje się ciecz. Jeżeli poziom cieczy jest utrzymywany stale na wysokości h, to ile wynosi stosunek prędkości wypływu cieczy w otworze górnym do prędkości wypływu cieczy w otworze dolnym?
|
h
v1 / v2 = ?
1. Równanie Bernoulliego
|
|
|
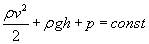
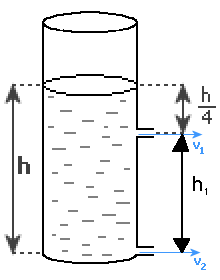 W zadaniu mamy podane założenie, że lustro wody jest utrzymywane na stałej wysokości h. Gdyby tego nie było w treści zadania, to dla poprawności rozwiązania należało by takie założenie poczynić oraz wykorzystać tzw. równanie ciągłości.
Teraz załóżmy, że wysokość naczynia jest na tyle mała, że ciśnienie atmosferyczne u podstawy naczynia, jak i na wysokości h są takie same, no i oczywiście jednorodność ośrodka (stałą gęstość w całej objętości naczynia).
I jeszcze trochę odnośnie oznaczeń, których będę używał w dalszej części:
1 będą parametryzowane wielkości charakteryzujące górny otwór,
2 - otworu u podstawy naczynia,
3 - lustra wody.
No to teraz możemy przystąpić do właściwego rozwiązania.
Równanie Bernoulliego przepiszemy w nieco innej formie :
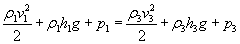
oraz
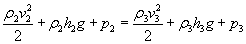
Teraz napiszę parę słów komentarza odnośnie powyższego wzoru. Pierwszy składnik sumy to tzw. ciśnienie dynamiczne związane z ruchem płynu, drugi, jak się pewnie domyślacie, ciśnienie hydrostatyczne, a trzeci ciśnienie zewnętrzne (w naszym przypadku tylko atmosferyczne).
Ponieważ gęstość jest stała, ciśnienie zewnętrzne na obu poziomach takie samo, prędkość opadania lustra wody równa zero, więc powyższe równania możemy dalej przekształcić.
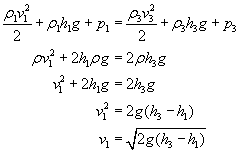
i
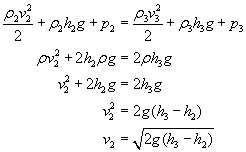
Z rysunku widzimy, że:
h1=h-h/4=3h/4
h2=0
h3=h
Uwzględniając te prawidłowości możemy powyższe wzory trochę uprościć.
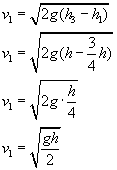
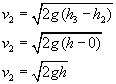
Ponieważ obie prędkości są uzależnione od tych samych wielkości, możemy więc stronami podzielić dwa ostatnie równania w celu policzenie szukanego stosunku.
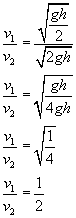
A wię stosunek tych prędkości to 1/2.
CIEKAWOSTKI
W ramach obliczeń prędkości wypływu wody z otworu, znajdującego się u podstawy naczynia, wyszła nam taka sama wartość, jak w przypadku obliczania prędkości końcowej w spadku swobodny z wysokości h. Ta własność nosi nazwę prawa Torricellego.
namyslowianin « powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
|
|
|
|
|
Serwis "Fizyka Jamnika" używa plików cookies. Są to pliki instalowane w urządzeniach końcowych osób korzystających z serwisu, w celu administrowania serwisem, poprawy jakości świadczonych usług w tym dostosowania treści serwisu do preferencji użytkownika, utrzymania sesji użytkownika oraz dla celów statystycznych i targetowania behawioralnego reklamy (dostosowania treści reklamy do Twoich indywidualnych potrzeb). Informujemy, że istnieje możliwość określenia przez użytkownika serwisu warunków przechowywania lub uzyskiwania dostępu do informacji zawartych w plikach cookies za pomocą ustawień przeglądarki lub konfiguracji usługi. Szczegółowe informacje na ten temat dostępne są u producenta przeglądarki, u dostawcy usługi dostępu do Internetu oraz w Polityce prywatności.
OK
|
|
