fizyka.org :: mamy 20 lat!

Strona główna Teoria Zadania Wzory Forum SzukajFAQ O nas

Strona główna > Zadania z fizyki > Gaz doskonały - teoria kinetyczno-molekularna, bilans cieplny > Zadanie 1

Gaz doskonały - teoria kinetyczno-molekularna, bilans cieplny - Zadanie 1

Treść:
Temperatura gazu idealnego wzrosła z T₁=T do T₂=nT. Jak zmieniła się średnia prędkość cząsteczek tego gazu?

Dane:
T₁ = T
T₂ = nT
k - stała Boltzmanna

Szukane:
v₂ / v₁ = ?

Wzory:
1. Energia kinetyczna

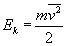
2. Średnia energia kinetyczna ruchu postępowego cząsteczek gazu doskonałego

Rozwiązanie:
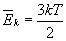
Kreseczka nad prędkością (v) oznacza, iż jest to średnia prędkość.
Pojawiająca się we wzorach literka k oznacza stałą Boltzmanna. Jej wartość można sprawdzić w tablicach :)

Aby obliczyć średnią prędkość cząsteczek gazu doskonałego, znając zmianę temperatury tego gazu, musimy obie wielkości powiązać ze sobą za pomocą energii kinetycznych. W przypadku gazu doskonałego, którego cząsteczki nie oddziałują ze sobą (z wyjątkiem chwil, w których się zderzają), za energię wewnętrzną uważamy tylko energię kinetyczną wszystkich rodzajów ruchu cząsteczek.
Skoro cząsteczki gazu posiadają jedynie energię ruchu postępowego (w tym przypadku jest to gaz jednoatomowy), możemy porównać oba wzory na energię.

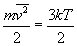
gdzie m to masa gazu.
Ze wzorów wyprowadzamy wzór na średnią prędkość cząsteczek gazu.

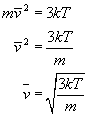
Mając już wyznaczoną prędkość wracamy do danych w zadaniu. Wiemy, że

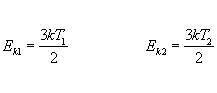
Podstawiając, że T₁=T i T₂=nT otrzymujemy:

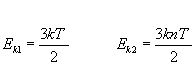
Z obu równań wyznaczamy prędkość (posługując się wcześniej otrzymanym wzorem):

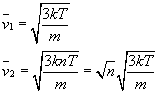
Szukaną zmianę prędkości wyrazimy poprzez stosunek średnich prędkości:

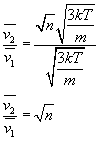
Prędkość cząsteczek gazu idealnego wzrosła o pierwiastek z n.

Itosu

« powrót do listy zadań

Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.

Teoria
Wyprowadzenia wzorów
Zadania fizyczne
Doświadczenia fizyczne
Tablice fizyczne
Biografie fizyków
FORUM
Oferty pracy

Gaz doskonały - teoria kinetyczno-molekularna, bilans cieplny

Potencjał spoczynkowy [0]
zadannie [0]
wykres energii potencjalnej w czasie [0]
Zadanie z elektrotechniki - rezystory [1]
fale elektromagnetyczne [0]

Serwis "Fizyka Jamnika" używa plików cookies. Są to pliki instalowane w urządzeniach końcowych osób korzystających z serwisu, w celu administrowania serwisem, poprawy jakości świadczonych usług w tym dostosowania treści serwisu do preferencji użytkownika, utrzymania sesji użytkownika oraz dla celów statystycznych i targetowania behawioralnego reklamy (dostosowania treści reklamy do Twoich indywidualnych potrzeb). Informujemy, że istnieje możliwość określenia przez użytkownika serwisu warunków przechowywania lub uzyskiwania dostępu do informacji zawartych w plikach cookies za pomocą ustawień przeglądarki lub konfiguracji usługi. Szczegółowe informacje na ten temat dostępne są u producenta przeglądarki, u dostawcy usługi dostępu do Internetu oraz w Polityce prywatności.


	strona główna :: o serwisie :: polityka prywatności :: reklama :: mapa serwisu :: wstecz :: do góry