Gaz doskonały ogrzano dostarczając ciepła Q. Temperatura bezwzględna wzrosła wskutek tego od wartości T do 3T, a ciśnienie od wartości p do 3p. Ile wyniósł przyrost energii wewnętrznej gazu?
|
Q
ΔT
Δp
ΔU = ?
1. Równanie gazu doskonałego
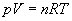
2. Energia wewnętrzna gazu doskonałego
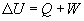
|
|
|
Nim dostarczono ciepło parametry gazu wynosiły p, T.
Zgodnie z pierwszym wzorem równanie gazu na początku moglibyśmy zapisać jako :
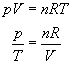
gdzie:
n - to liczba cząsteczek gazu (w naszym zadaniu niezmienna),
R - stała gazowa,
V - objętość, jaką zajmował ten gaz.
Po dostarczeniu ciepła temperatura wzrosła do 3T, a ciśnienie do 3p.
Zapiszmy równanie gazu dla tych warunków:
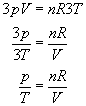
Jak widzimy objętość gazu nie zmieniła się. Można by zapytać co to ma wspólnego z przyrostem energii wewnętrznej gazu, który mamy określić? Ma, i to bardzo dużo :)
By obliczyć przyrost energii wewnętrznej gazu musimy znać ilość dostarczonego ciepła i pracę jaką wykonano nad gazem, bądź jaką on wykonał. Ilość ciepła mamy podaną w treści zadania, zaś jedyną niewiadomą jest praca. Jeśli wykonalibyśmy pracę nad gazem musielibyśmy poruszyć tłokiem i sprężyć gaz, zaś jak gaz wykonałby pracę, musiałby również "poruszyć" tłokiem. Wykazaliśmy, że objętość gazu przed i po dostarczeniu mu ciepła nie zmieniła się więc tłok cały czas był w jednej pozycji, czyli:
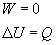
Ostatecznie możemy odpowiedzieć, że przyrost energii wewnętrznej gazu wynosi Q.Jawor
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
