Takie same ładunki Q znajdują się w każdym rogu kwadratu o boku a. Poszczególne ładunki zostają uwalniane
pojedynczo zgodnie z ruchem wskazówek zegara. Uwalniany ładunek osiąga swoją końcową prędkość zanim kolejny
ładunek zostanie uwolniony. Jakie są końcowe energie kinetyczne wszystkich czterech ładunków?
|
Q
a - bok kwadratu
k - stała
EK = ?
1. Potencjał elektrostatyczny:
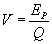
2. Potencjał elektrostatyczny:
|
|
|
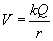
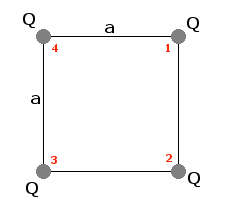Na rysunku czerwonymi cyframi zaznaczono kolejność "wypadania" ładunków.
Przy rozwiązywaniu zadania korzystamy z zasady zachowania energii. Gdy na początku ładunek znajduje się w wierzchołku kwadratu posiada on energię potencjalną pola elektrostatycznego, ale nie posiada energii kinetycznej, ponieważ prędkość ładunku równa jest zeru. Gdy ładunek zacznie się oddalać, dotrze on do takiego punktu, w którym energia potencjalna jest równa zeru (punkt taki, zgodnie z teorią, znajduje się nieskończenie daleko). Wtedy całkowita początkowa energia potencjalna zostanie zamieniona na energię kinetyczną. Tak więc za każdym razem:
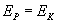Musimy zastanowić się, jak wyznaczyć energię potencjalną w polu elektrostatycznym. Nie jest to trudne, należy skorzystać ze wzoru pierwszego, który przekształcamy do postaci:
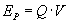gdzie V jest potencjałem elektrostatycznym, który wyznaczamy ze wzoru:
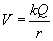Najpierw zajmujemy się ładunkiem pierwszym. Potencjałem całkowitym jest tutaj suma potencjałów pochodzących od każdego ładunku (zgodnie z zasadą superpozycji):
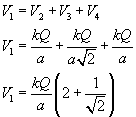Zauważmy, że przy ładunku trzecim odległością jest długość przekątnej kwadratu, a w pozostałych przypadkach - długość boku kwadratu.
Wyliczamy energię potencjalną
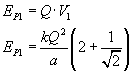A ponieważ EK = EP
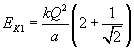Teraz gdy ładunek pierwszy jest daleko w nieskończoności, to nie wpływa on na pozostałe ładunki, tak więc pozostały nam trzy ładunki.
W podobny sposób liczymy energie kinetyczne dla pozostałych ładunków:
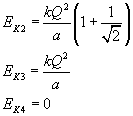Słowo wyjaśnienia należy się w przypadku ostatnim. Otóż wtedy zostaje nam tylko jeden ładunek, bo pozostałe są w nieskończoności. W takim wypadku ładunek ten nie ma z czym oddziaływać, a więc pozostaje w spoczynku. Wtedy energia kinetyczna równa jest zeru.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
