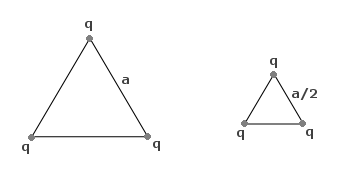
W każdym wierzchołku trójkąta równobocznego o boku a umieszczono ładunek q i w ten sposób wykonano łącznie pracę W. Jakiej pracy wymaga zbudowanie takiego samego trójkąta o boku a/2?
|
a - bok trójkąta
q
W
W' = ?
1. Praca w polu elektrostatycznym:
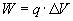
2. Potencjał elektrostatyczny:
|
|
|
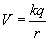
Aby obliczyć pracę, korzystamy z jednego ze wzorów na pracę w polu elektrostatyczną. My wybraliśmy wzór
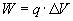Za ΔV przyjmiemy całkowity potencjał pola, który wyliczymy z zasady superpozycji potencjałów, która mówi, że potencjał całkowity równy jest sumie algebraicznej potencjałów składowych.
Spójrzmy najpierw na trójkąt o boku a.
Na każdy ładunek q działają dwa inne ładunki oddalone w każdym przypadku o a. Potencjał wyliczony dla jednego z ładunków q wynosi:
A ponieważ takich ładunków mamy trzy sztuki, to całkowity potencjał wynosi
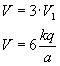Pamiętajmy, że k to stała zależna od środowiska, w którym znajdują się ładunki - jednak, jak zobaczycie później, ona wcale nie będzie nam potrzebna.
Wykonana praca przy budowie trójkąta pierwszego
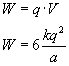
Teraz zajmiemy się trójkątem o boku a/2.
Rzecz z potencjałami ma się identycznie jak poprzednio.
Potencjał w punkcie pola, w którym znajduje się jeden z ładunków wyrażamy...
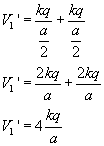a ponieważ mamy trzy ładunki, to:
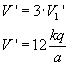Czyli wykonana praca wynosi:
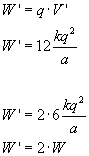Tak więc aby zbudować trójkąt o boku a/2 należy wykonać dwa razy większą pracę, niż przy budowie trójkąta o boku a.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
