Kulę przewodzącą o promieniu r, naładowaną do potencjału V, zetknięto z nienaelektryzowaną kulą o trzykrotnie większym promieniu. Ile wynosi potencjał kul po zetknięciu?
|
r
R = 3r
V
V' = ?
1. Potencjał:
|
|
|
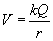
Skorzystamy tutaj z zasady zachowania ładunku. Otóż ładunek który znajdował się w kuli o promieniu r będzie równy ładunkowi, jaki będzie umieszczony w dwóch kulach po zetknięciu.
Przed zetknięciem mamy daną kulę o promieniu r. Jej potencjał wynosi
Ze wzoru na potencjał wyprowadzono obok wzór na ładunek.
Stykamy teraz naszą kulę z nienaładowaną kulą (czyli o potencjale równym zeru) o promieniu 3r.
Powstała różnica potencjałów, zatem układ nie jest w równowadze elektrostatycznej. Następuje przemieszczanie się elektronów swobodnych w stronę potencjału wyższego, aż do memontu wyrównania się potencjałów obu kul, który oznaczymy przez V'.
Ale oczywiście pozostał ten sam ładunek, który znajduje się teraz w dwóch kulach:
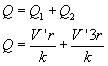Porównujemy dwa powyższe wzory na ładunek
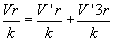Równanie to możemy uprościć przez stałą k, promień r oraz wyliczyć szukany potencjał kul po zetknięciu
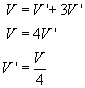Potencjał kul po zetknięciu jest równy 0.25 potencjału naładowanej kuli przed zetknięciem.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
