Pomiędzy okładki kondensatora próżniowego, równolegle do jego okładek, zostaje wstrzelony proton o szybkości v0=10000m/s. Oblicz przyrost energii kinetycznej protonu po przejściu przez kondensator, jeżeli odległość między okładkami wynosi d=5mm, napięcie między nimi U=1200V, a długość okładek l=0.05m.
|
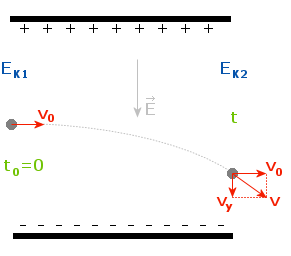Cząstką, którą wstrzeliwujemy do kondensatora, jest proton, którego masę m oraz ładunek q podajemy z tablic fizycznych
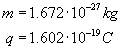Sytuacja z zadania przedstawiona jest na powyższym rysunku.
Otóż proton wchodzi do kondensatora z prędkością v0. Ponieważ proton ma ładunek dodatni, to wewnątrz kondensatora jest on przyciągany przez okładkę ujemną i tor ruchu zakrzywia się (sytuacja podobna do rzutu poziomego).
Gdy proton wyjdzie z kondensatora porusza się on z prędkością v, którą możemy rozłożyć na składowe:
- w kierunku poziomym proton porusza się ruchem jednostajnym prostoliniowym z prędkością v0,
- w kierunku pionowym proton porusza się ruchem jednostajnie przyspieszonym z prędkością vy.
W zadaniu mamy policzyć zmianę energii kinetycznej
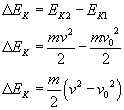Musimy zatem znaleźć prędkość v, która jest wypadkową prędkości v0 i vy (patrz rysunek)
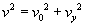Wzór na zmianę energii przybierze postać:
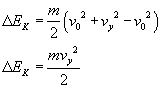Jak się okazuje, naszym głównym zadaniem jest znalezienie prędkości vy.
Prędkość ta pojawia się wskutek działania pola elektrostatycznego jednorodnego wewnątrz kondensatora, które wyrazić możemy na dwa sposoby. Pole elektrostatyczne jednorodne to stosunek napięcia U panującego pomiędzy okładkami do odległości d tych okładek
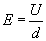Jednocześnie pole elektrostatyczne to stosunek siły działającej wzdłuż linii sił pola na ładunek do wartości tego ładunku
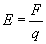Porównujemy nasze wzory; siłą F będzie siła powodująca przyciąganie protonu do okładki ujemnej
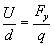Ponieważ w kierunku pionowym mamy do czynienia z ruchem jednostajnie przyspieszonym, to siłę tę możemy wyrazić poprzez drugą zasadę dynamiki:
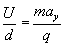Przyspieszenie to stosunek prędkości do czasu
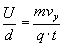No tak, ale nie mamy jeszcze czasu t. Aby znaleźć ten czas, skorzystamy z ruchu poziomego (ruch jednostajny prostoliniowy). Po tym samym czasie t wartość drogi w tym ruchu wynosi
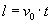stąd czas t:
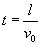Czyli nasze równanie przybiera postać:
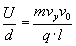Wszystko już mamy dane, możemy w takim razie wyprowadzić wzór na vy...
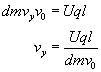...i znaleźć wartość szukanej zmiany energii kinetycznej:
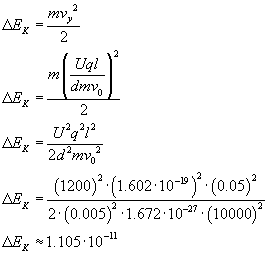Przy tak wyrafinowanym wzorze warto sprawdzić poprawność jednostki
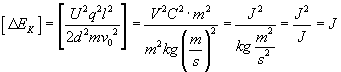Przyrost energii kinetycznej wynosi około 1.105 . 10-11 J.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
