Drut o oporze 8Ω rozciągnięto do długości dwukrotnie większej niż początkowa. Ile wyniesie opór rozciągniętego drutu, jeżeli podczas rozciągania nie zmieniają się ani opór właściwy ani gęstość materiału?
|
R = 8 Ω
ρ = const (opór właściwy)
G = const (gęstość)
l' = 2l
R' = ?
1. Opór przewodnika (z uwzględnieniem oporu właściwego)
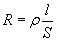
2. Gęstość
|
|
|
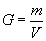
Zadanie nie jest takie trudne, jednak łatwo w nim się pomylić.
Na pewno skorzystamy ze wzoru, w którym zarówno występuje opór elektryczny i opór właściwy
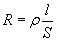gdzie:
R - opór elektryczny,
ρ - opór właściwy,
l - długość przewodnika,
S - pole przekroju przewodnika.
Nie mamy danego pola przekroju, a jak wiadomo, skoro przewodnik się wydłuża, to jego pole przekroju musi się zmniejszyć. A jak liczbowo prezentują się te zmiany? Sprawdzimy to, korzystając z tego, że pole przekroju przewodnika S razy jego długość l to nic innego, jak objętość V
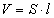Przekształcamy ten wzór...
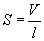...i podstawiamy go do wzoru na opór
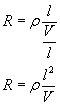Powinniśmy się jeszcze zastanowić, czy zmienia się objętość przewodnika. Intuicyjnie wydaje się, że nie - ale we fizyce wszystko musi być udowodnione. Jak to zrobić? Ano wiemy jeszcze, że gęstość G materiału (czyli ilorazu masy przez objętość), z którego wykonany jest przewodnik nie zmienia się. Ze wzoru na gęstość...
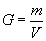...wyprowadzamy objętość...
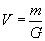...i wstawiamy to wszystko do wzoru na opór:
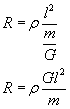A przecież po rozciągnięciu masa drutu na pewno się nie zmieni!
Liczymy więc opór drutu przed rozciąganiem...
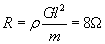i szukany opór po rozciągnięciu:
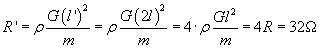Wykorzystujemy oczywiście to, że stałe są wartości charakteryzujące przewodnik: opór właściwy ρ, gęstość G oraz masa m.
Sprawdzimy jeszcze tylko, czy wzór generuje poprawną jednostkę, a co za tym idzie czy jest poprawny
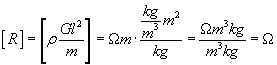Opór rozciągniętego drutu wynosi 32 omów.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
