Policzyć opory zastępcze dla przedstawionych układów oporników o oporze R każdy.
|
R
RZ = ?
1. Szeregowe i równoległe łączenie oporników
|
|
|
a)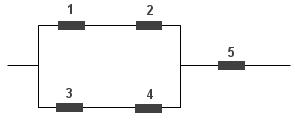
Najpierw policzymy opory zastępcze szeregowego połączenia oporników 1 i 2 oraz 3 i 4:
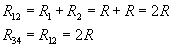Te opory zastępcze tworzą układ równoległy, którego opór zastępczy wynosi:
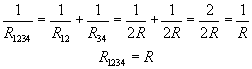Pozostaje nam wyliczenie oporu zastępczego całego układu oporników (teraz mamy układ szeregowy)
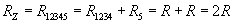
b)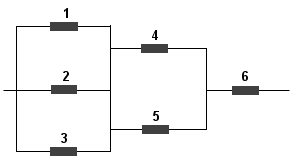
Jeśli ktoś powie, że powyższy układ sprawia wrażenie trudnego, to ma rację - rzeczywiście tylko sprawia takie wrażenie. W rzeczywistości zadanie jest banalne, wystarczy zauważyć, że poniższy układ jest identyczny z powyższym:
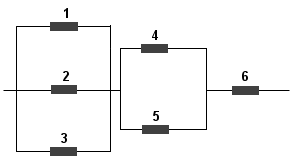Tak więc liczymy opór zastępczy układów równoległych złożonych z oporników 1, 2 i 3 oraz 4 i 5:
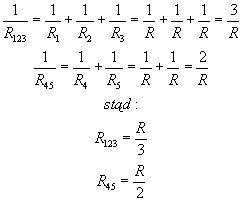Powstaje nam układ szeregowy, którego opór zastępczy wynosi:
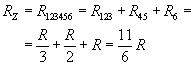
c)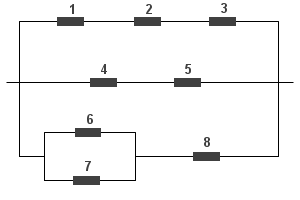
Najpierw policzymy opór układu równoległego kondensatorów 6 i 7:
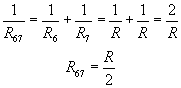Teraz mamy szeregowe układy kondensatorów: 1-2-3, 4-5, 67-8. Liczymy ich opory:
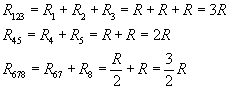Z powyższych układów utworzył nam się układ równoległy, po wyliczeniu jego oporu otrzymamy opór zastępczy:
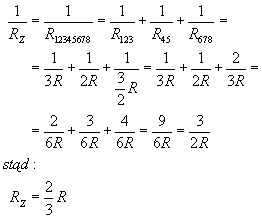
d)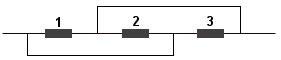
Zastanówmy się jak zachowuje się prąd elektryczny. Skoro mamy jednakowe oporniki o oporze R każdy, to prąd będzie chciał przepływać przez jak najmniejszą liczbę oporników. W naszym przypadku prąd może przepływać przez jeden z oporników na trzy różne sposoby:
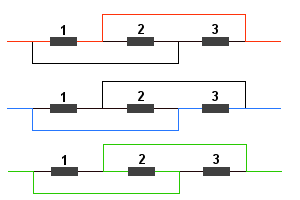Spróbujmy narysować nasz układ w nieco inny sposób
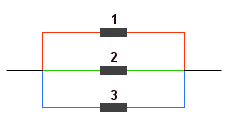I w ten sposób zadanie stało się... proste. :) Liczymy opór zastępczy:
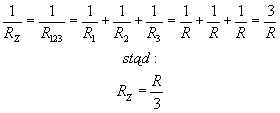
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
