Odległość między dwoma miastami wynosi s = 300 km. Z każdego z nich w tej samej chwili wyrusza pociąg w stronę drugiego miasta. Jakie drogi przebędą pociągi do chwili spotkania, jeśli szybkości wynoszą odpowiednio v1 = 100 km / h oraz v2 = 50 km / h
|
v1 = 100 km / h
v2 = 50 km / h
s1 = ? - droga
pociągu 1
s2 = ? - droga
pociągu 2
Wzór na drogę:
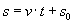
Wzór na prędkość:
|
|
|
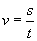
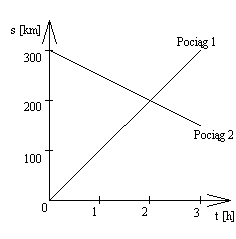Zależność odległości pociągów od miast możemy przedstawić na wykresie, jak powyżej. Chwila spotkania się pociągów, to punkt w którym przecinają się obie proste. Proste, które przedstawiają drogę pociągów, możemy opisać wzorami:
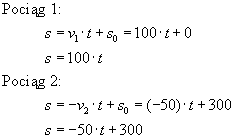
Należy zauważyć, że:
a) s0 dla pociągu 1 wynosi zero, ponieważ przyjeliśmy, że miasto z którego wyjeżdża, leży w punkcie zero
b) s0 dla pociągu 2 wynosi 300, ponieważ jest to pociąg, który wyjeżdża z miasta odległego o 300 km od drugiego miasta
c) v2 ma wartość ujemną we wzorze, ponieważ pociąg jedzie w stronę miasta leżącego w punkcie zero, więc tak jakby wracał, co też widać na wykresie (wykres jest malejący).
Teraz należy rozwiązać układ równań utworzony przez dwa równania drogi: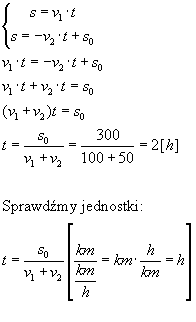
Teraz już wiemy, że pociągi spotkają się po 2 h. Aby wyliczyć drogę jaką przejechały przez ten czas należy skorzystać ze wzoru na prędkość i odpowiednio go przekształcić:
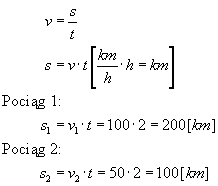Odpowiedź: Pociągi spotkają się po 2 h, więc w tym czasie pociąg 1 przejedzie drogę s1 = 200 km, a pociąg 2 przejedzie s2 = 100 km Zajec
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
