Korzystając z wykresów przedstawiających zależność prędkości od czasu oblicz:
w jakiej odległości od punktu startu znajduje się ciało po 40 s w pierwszym,
a po 6 s w drugim przypadku. Jaka będzie średnia szybkość w zadanych przedziałach czasu.
|
Wzór na prędkość:
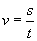
Wzór na prędkość średnią:
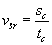
gdzie:
sc - droga całkowita
tc - czas całkowity
|
|
|
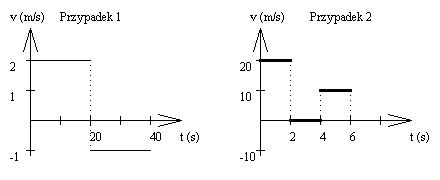
Przypadek 1:
Wykres możemy podzielić na dwa etapy. Pierwszy etap to gdy ciało przemieszczało się z prędkością v1 = 2 m / s i drugi etap to, gdy ciało miało prędkość v2 = -1 m / s. Wartość ujemna prędkości oznacza, że ciało wracało - czyli zbliżało się do punktu startu.
Bez problemu z wykresu możemy odczytać ile czasu trwały poszczególne etapy:
etap I trwał t1 = 20 s
etap II trwał t2 = 40 - 20 = 20 s
Znając te dane i odpowienio przekształcając wzór na prędkość możemy obliczyć odległość ciała od punktu startu: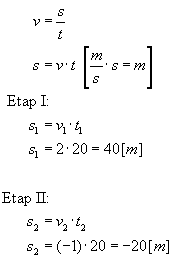 
Mając obliczoną drogę przejechaną na poszczególych etapach, wystarczy ją teraz tylko z sumować, aby wyliczyć w jakiej odległości od startu znajduje się ciało:
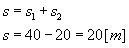Do obliczenia prędkości potrzebujemy drogi całkowitej, która jest sumą wartości bezwzględnych odległości przejechanych w poszczególnych etapach:
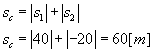Czas całkowity wynosi:
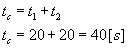Teraz wystarczy już tylko podstawić do wzoru na prędkość średnią: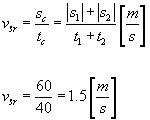
Przypadek II:
Ruch dzielimy na 3 etapy. Każdy etap trwa tyle samo, tzn. t1 = t2 = t3 = 2 s. Prędkości w poszczególnych etapach możemy odczytać bez problemu z wykresu i wynoszą:
v1 = 20 m / s, v2 = 0 m / s, v3 = 10 m / s.
Znając prędkości i czasy trwania poszczególnych etapów, ze wzoru na prędkość wyliczamy drogę przejechaną na każdym odcinku:
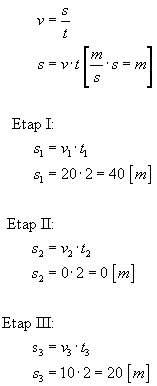Mamy wyliczone odległości przejechane w poszczególnych etapach. Teraz wystarczy je z sumować, aby otrzymać w jakiej odległości od punktu startu znajduje się ciało: 
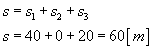W tym przypadku odległość od punktu startu jest równa drodze całkowitej, ponieważ ciało poruszało się tylko w jednym kierunku. Znamy także czas całkowity (suma czasów wszystkich etapów). Tak więc możemy wyliczyć prędkość średnią: 
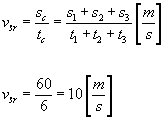Odpowiedź:
Przypadek 1: Ciało po 40 sek znajduje się w odległości 20 metrów od punktu startu, a vśr = 1.5 m / s
Przypadek 2: Ciało po 6 sek znajduje się w odległości 60 metrów od punktu startu, a vśr = 10 m / s
Zajec
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
