Cząstka α wpada w pole magnetyczne o indukcji B=0.02T prostopadle do kierunku wektora indukcji B i zatacza krąg o promieniu r=0.2m. Oblicz energię cząstki (w J i keV).
|
Skąd się bierze zorza polarna? Pokrótce dlatego, że Ziemia posiada własne pole magnetyczne (niezbędne dla życia), które naładowane cząsteczki pochodzące ze Słońca "ściąga" na bieguny.
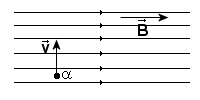
Tak samo zachowuje się cząstka α w naszym zadaniu, która wpada w pole magnetyczne o idukcji B. Mając prędkość v zatacza ona krąg o promieniu r.
Siłą zakrzywiającą jest siła Lorenza. Możemy to przedstawić następująco:
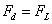
czyli:
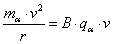
Skracamy jedno v i wyliczamy prędkość tej cząstki:
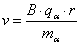
Prędkość nie jest tak duża, że trzeba używać wzorów relatywistycznych, dlatego użyjemy zwykłego wzoru na energię:
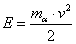
Podstawiając otrzymaną prędkość dostajemy:
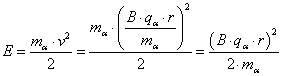
Tak otrzymaliśmy ostateczny wzór na energię tej cząstki. Wiemy, że cząstka α jest po prostu jądrem atomu helu. Tak więc posiada 2 protony i 2 neutrony.
Z tego wnioskujemy, że masa jest równa w przybliżeniu 4 masom protonu (dla dokładności obliczeń masę cząstki odczytujemy z tablic). Jeśli chodzi o ładunek to łatwo się domyślamy, że wyniesie q=+2e.
Teraz już mamy wszystko, aby obliczyć energię. Na początku użyjmy podstawowych jednostek układu SI (czyli ładunek będzie w C):
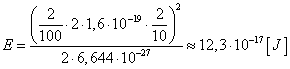
Sprawdźmy jeszcze jednostkę:
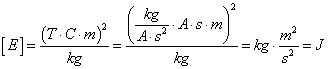
Aby obliczyć energię w eV musimy znaleźć związek między eV oraz J. Skorzystajmy wpierw na wzór podany powyżej na energię przejścia ładunku q przez potencjał U.
Energia ta jest równa 1J, gdy ładunek będzie równy 1C (korzystamy tutaj z energii kondensatora) . A więc przy przejściu tego ładunku przez potencjał 1U więc stwierdzamy, że:
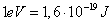
czyli:
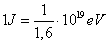
Energia wyniesie więc:
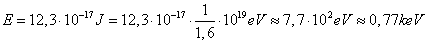
Energia cząstki α wynosi E=12,3 . 10-17J (0,77 keV).marcyk
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
