Obwód prądu zmiennego składający się z połączonych ze sobą opornika R=16Ω oraz cewki o indukcyjności L=12H, zasilany jest sinusoidalnie zmiennym prądem. Amplituda napięcia jest równa U0=50V, a jego częstotliwość wynosi f=1/(2π)Hz. Oblicz: zawadę obwodu, amplitudę płynącego w nim prądu, przesunięcie fazowe napięcia względem prądu oraz wydzielaną moc skuteczną w obwodzie.
|
W treści zadania mamy podane, iż nasz obwód elektryczny składa się z opornika i cewki. Taki obwód nazywamy obwodem RL. Policzmy najpierw przesunięcie fazowe. W takim obwodzie napięcie wyprzedza w fazie natężenie prądu o kąt φ, którego tangens wynosi:
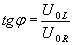gdzie:
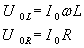zatem:
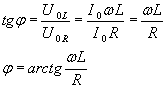
Żeby obliczyć częstość kołową, skorzystajmy wprost z wzoru 6:
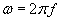
Podstawiając to do wzoru na przesunięcie fazowe otrzymujemy:
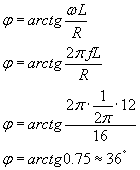
Obliczyliśmy już przesunięcie fazowe, a teraz zajmiemy się wyliczeniem impedancji, zwanej inaczej zawadą ZRL, która z definicji wynosi:
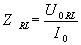Wartość U0RL mamy daną, ale niestety nie mamy I0. Jak to naprawić? Spróbujmy rozpisać nasze natężenie U0RL:
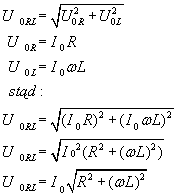...aby ostatecznie wyliczyć naszą zawadę:
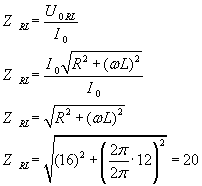
Na koniec sprawdźmy poprawność jednostki (powinien wyjść om):
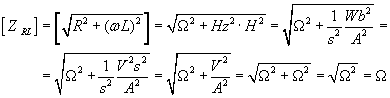Udało się! :)
Teraz czas na amplitudę, czyli maksymalną wartość natężenia. Wyliczymy ją przekształcając poprzedni wzór na zawadę (tym razem nie rozpisujemy już U0RL):
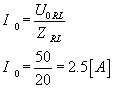
Ostatnią niewiadomą jaka nam została jest moc skuteczna (wzór 2 przekształcimy korzystając z prawa Ohma):
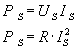
Aby obliczyć natężenie skuteczne IS skorzystajmy z zależności między natężeniami: maksymalnym (amplitudą) i skutecznym:
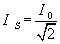
Wstawiamy powyższe do wzoru na moc średnią i wyliczamy ją:
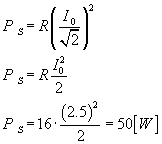
Chyba nie było aż tak źle, jak wyglądało to na początku. :)
Ostatecznie otrzymaliśmy, że impedancja (zawada) wynosi 20 omów, amplituda 2.5 A, przesunięcie fazowe około 36 stopni, a moc skuteczna 50 watów.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
