Napisz równane opisujące ruch:
a) wahadła matematycznego o długości l=0.5m, o amplitudzie A=0.1m,
b) ciężarka o masie m=0.01kg umocowanego na sprężynce, wykonującego drgania w płaszczyźnie
poziomej z amplitudą A=0.02m; współczynnik sprężystości sprężynki k=1N/m,
c) małej kuleczki zawieszonej na długiej nitce przyczepionej do statywu wykonującej drgania harmoniczne o okresie T=0.2s i
amplitudzie A=0.005m.
|
Potrzebujemy w obu przypadkach znaleźć wzór opisujący ruch ciała drgającego. Ruch ten wyraża wychylenie x, które jest zależne od upływającego czasu t.
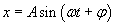Pozostałe wartości:
A - amplituda,
ω - częstość kołowa,
φ - faza początkowa,
są stałe i to właśnie je znajdziemy, by wyrazić nasze równanie.
W obu przypadkach faza początkowa nie odgrywa żadnej roli, więc uznamy że jest równa zeru. Wobec tego:
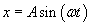
Przypadek a)
Mamy wahadło matematyczne, czyli nić o długości l na której zawieszony jest ciężarek wykonujący drgania o amplitudzie A. Aby uzupełnić nasze równania potrzebujemy znaleźć ω. Wiemy, że:
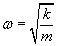Z drugiej strony stałą k w wahadle matematycznym wyrażamy jako:
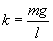Stąd łącząc oba wzory:
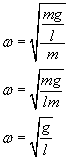gdzie g to przyspieszenie ziemskie (9.8 m/s2).
Zatem nasze równanie przyjmie ostatecznie postać:
Przypadek b)
A teraz sprężyna. Tutaj korzystamy z wzoru
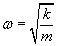Wtedy równanie ruchu:
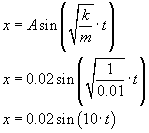
Przypadek c)
Znów mamy wahadło matematyczne. Tym razem mamy podany okres, ale przecież:
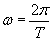Zapisanie równania ruchu nie powinno sprawić trudności:
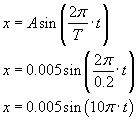Zauważ, że w wahadle matematycznym równanie ruchu nie zależy od masy ciężarka. Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
