Ile wynosi okres drgań punktu materialnego drgającego ruchem harmonicznym prostym, dla którego po czasie 1s wychylenie z położenia równowagi wynosi sqrt(2).A/2, gdzie A to amplituda? sqrt(2) oznacza pierwiastek z dwóch.
|
x = sqrt(2) . A / 2
t = 1 s
T = ?
1. Wychylenie w ruchu harmonicznym prostym
|
|
|
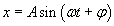
W większości zadań będziemy przyjmować, że faza początkowa φ jest równa zeru, chyba że będzie napisane inaczej. Mamy znaleźć okres T drgań jakiegoś punktu materialnego.
Korzystamy oczywiście ze wzoru na wychylenie w ruchu harmonicznym (drgającym) oraz uwzględniamy, że φ = 0:
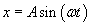A gdzie tu jest okres T? Oczywiście ukryty. ;)
Trzeba bowiem wiedzieć, że stałą ω wyrażamy jako:
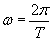Czyli reasumując, wychylenie jest równe:
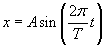Skorzystajmy, z tego, że
Przyrównujemy dwa powyższe wzory
Teraz przydadzą się nam wiadomości z trygonometrii. Otóż już od gimnazjum wiadomo, że:
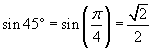Wykorzystujemy to do powyższego:
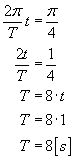Zatem okres drgań punktu materialnego wynosi 8 sekund.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
