Punkt materialny wykonuj±cy drgania harmoniczne o okresie T jest w chwili czasu t=0 w maksymalnej odleg³o¶ci od po³o¿enia równowagi. Po jakim czasie odleg³o¶æ ta zmaleje do po³owy?
|
T
gdy t = 0, to x = A
t = ?
1. Wychylenie w ruchu harmonicznym prostym:
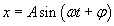
2. Wzory redukcyjne
|
|
|
Najpierw zajmiemy siê chwil± pocz±tkow± t = 0. Wtedy równanie na wychylenie przyjmuje postaæ
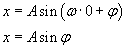Wiemy jeszcze, ¿e w chwili t = 0 punkt znajdowa³ siê w maksymalnej odleg³o¶ci od po³o¿enia równowagi, czyli punkt osi±gn±³ amplitudê A. Zatem:
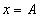Oznacza to, ¿e
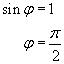Je¿eli co¶ jest niejasne, proponujê zajrzeæ do Zadania 3 z tego dzia³u.
Teraz poszukamy warto¶æ chwili t, w którym odleg³o¶æ x zmaleje do po³owy warto¶ci z chwili t = 0, czyli bêdzie wynosiæ pó³ amplitudy.
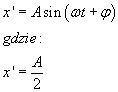St±d otrzymamy, ¿e
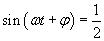Podstawiamy wyliczon± wcze¶niej warto¶æ fazy pocz±tkowej φ
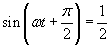I znów potrzebna nam jest trygonometria. Dodaj±c k±t φ do warto¶ci ωt wychodzimy poza pierwsz± æwiartkê uk³adu wspó³rzêdnych. Dlatego warto skorzystaæ z tzw. wzorów redukcyjnych, które umo¿liwiaj± nam powrót do pierwszej æwiartki. Jeden ze wzorów mówi, ¿e:
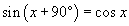Oczywi¶cie 90o to to samo co π/2, mam nadziejê, ¿e wiesz to z matematyki. Stosujemy wiêc powy¿sze i otrzymujemy:
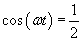Jeste¶my w pierwszej æwiartce, a wiêc:
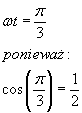Teraz sta³± ω wyrazimy poprzez warto¶æ z okresem T, który mamy dany
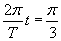I znajdujemy szukany czas t:
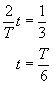Odleg³o¶æ zmaleje do po³owy warto¶ci amplitudy po czasie równym T/6.
Jamnik
« powrót do listy zadañZnalaz³e¶ b³±d w materiale? Skontaktuj siê z nami, przysy³aj±c adres strony, na której znajduje siê b³±d i informacjê o tym, czego dotyczy b³±d.
