Punkt materialny wykonuje drgania harmoniczne o amplitudzie A i okresie T. Jak zmieni się maksymalna energia kinetyczna, jeżeli zwiększymy dwukrotnie okres drgań, a amplituda nie zmieni się?
|
A = A'
2T = T'
EKmax / EKmax' = ?
1. Energia kinetyczna maksymalna:
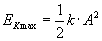
2. Wzory na stałą ω (częstość kołową):
|
|
|
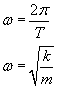
Na początku mieliśmy drgania o amplitudzie A i okresie T. Wskutek tego uzyskaliśmy pewną wartość maksymalnej energii kinetycznej, którą wyrażamy wzorem:
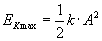za chwilę pomajstrujemy w tym wzorze, bo zmieni się nam okres T. Ale zaraz, gdzie tu jest ten okres? No właśnie - trzeba go wyprowadzić. :]
Spójrzmy na dwa wzory na częstość kołową ω. Nic nie stoi na przeszkodzie, by je porównać:
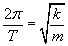Podnieśmy obie strony do kwadratu i wyprowadźmy wzór na stałą k...
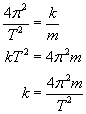...który będziemy mogli podstawić do wzoru na maksymalną energię kinetyczną:
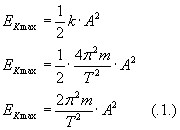Tak więc mamy potrzebny nam wzór na energię kinetyczną maksymalną, uwzględniający okres i amplitudę.
Teraz dokonujemy zmian:
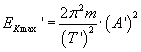Ponieważ amplituda się nie zmienia, a T' = 2T, to:
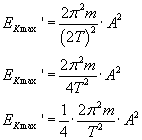A teraz wykorzystując fakt (.1.), otrzymamy szukany stosunek.
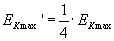Po zwiększeniu dwukrotnie okresu, maksymalna energia kinetyczna zmaleje czterokrotnie.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
