Znajdź temperaturę pieca, jeżeli wiadomo, że z otworu o powierzchni 4cm2 promieniuje w ciągu 1 sekundy energia 22.7J. Promieniowanie otworu przyjąć za bliskie promieniowaniu ciała doskonale czarnego.
|
S = 4 cm2
t = 1 s
E = 22.7 J
T = ?
1. Prawo Stefana-Boltzmanna
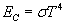
|
|
|
Ciało doskonale czarne? Nie mamy wyjścia - musimy skorzystać z prawa Stefana-Boltzmanna. Mówi ono, że energia emitowana w jednostce czasu z jednostki powierzchni jest proporcjonalna do czwartej potęgi temperatury bezwzględnej (czyli w stopniach Kelvina)
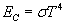
Co oznacza jednostka czasu i jednostka powierzchni? To, że powyższy wzór jest słuszny, gdy energia emitowana jest w ciągu jednej sekundy z jednego metra kwadratowego powierzchni. Inaczej więc można powyższy wzór zapisać jako:
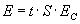
Tak wyrażona energia E jest energią w dżulach i wyliczenie temperatury pozostaje tylko formalnością:
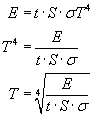
σ to stała Stefana, powierzchnię natomiast musimy przeliczyć:
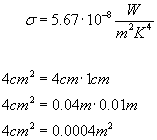
Tak więc szukana temperatura:
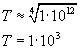
Sprawdzimy jeszcze dla pewności poprawność jednostki - powinien wyjść Kelvin:
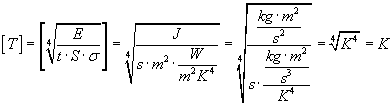
Wszystko się zgadza, więc piec ma temperaturę około 1000 K.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
