fizyka.org :: mamy 19 lat!

Strona główna Teoria Zadania Wzory Forum SzukajFAQ O nas

Strona główna > Zadania z fizyki > Kinematyka ruchu obrotowego > Zadanie 6

Kinematyka ruchu obrotowego - Zadanie 6

Treść:
Oblicz promień R obracającej się tarczy, jeżeli przy prędkości liniowej v₁ punktów na obwodzie, punkty znajdujące się w odległości od środka r₂ = R - x poruszają się z prędkością v₂.

Dane:
v₁ [m/s]
v₂ [m/s]
r₂ = R - x [m]

Szukane:
R

Wzory:
1. Wzór na obwód:

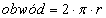
2. Wzór na prędkość liniową z wykorzystaniem obwodu i częstotliwości:

Rozwiązanie:
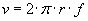
z danych, które mamy możemy obliczyć obwód małego koła: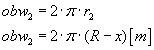

Aby wyliczyć częstotliowść tarczy (f)należy podzielić prędkość liniową przez obwód koła:

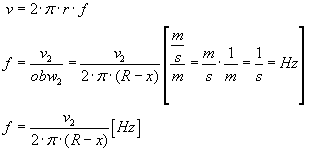Następnie wykonując analogiczne obliczenia dla koła o promieniu R uzyskujemy wzór na częstotliwość, w którym będzie wykorzystana prędkość v₁:

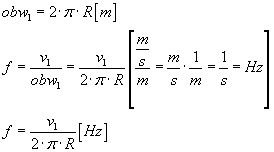Uzyskaliśmy dwa wzoru na częstotliwość. Jednak obie te częstotliwości muszą być sobie równe, ponieważ oba koła (duże i małe) znajdują się na tej samej tarczy, tak więc obracają się z tą samą częstotliwościa:

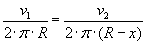Teraz, wykonując już tylko proste przekształcenia, możemy wyliczyć promień R:

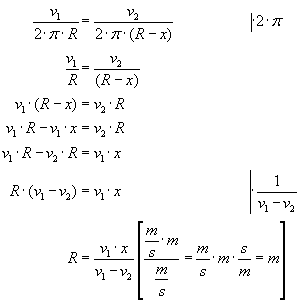Odpowiedź:
Promień R wynosi: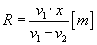

Zajec

« powrót do listy zadań

Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.

Teoria
Wyprowadzenia wzorów
Zadania fizyczne
Doświadczenia fizyczne
Tablice fizyczne
Biografie fizyków
FORUM

Rozkład Plancka [0]
Co powoduje dylatację czasu [0]
siły dziłające na liny [0]
Gazy [1]
Punkt materialny - hellp me [0]

Serwis "Fizyka Jamnika" używa plików cookies. Są to pliki instalowane w urządzeniach końcowych osób korzystających z serwisu, w celu administrowania serwisem, poprawy jakości świadczonych usług w tym dostosowania treści serwisu do preferencji użytkownika, utrzymania sesji użytkownika oraz dla celów statystycznych i targetowania behawioralnego reklamy (dostosowania treści reklamy do Twoich indywidualnych potrzeb). Informujemy, że istnieje możliwość określenia przez użytkownika serwisu warunków przechowywania lub uzyskiwania dostępu do informacji zawartych w plikach cookies za pomocą ustawień przeglądarki lub konfiguracji usługi. Szczegółowe informacje na ten temat dostępne są u producenta przeglądarki, u dostawcy usługi dostępu do Internetu oraz w Polityce prywatności.


	strona główna :: o serwisie :: polityka prywatności :: reklama :: mapa serwisu :: wstecz :: do góry