fizyka.org :: mamy 22 lat!

Strona główna Teoria Zadania Wzory Forum SzukajFAQ O nas

Strona główna > Zadania z fizyki > Zasady dynamiki Newtona > Zadanie 18

Zasady dynamiki Newtona - Zadanie 18

Treść:
Ciało o masie m jest hamowane siłą proporcjonalną do prędkości F=-kv. W chwili t=0 ciało miało prędkość v₀. Zapisz i rozwiąż równanie ruchu. Znajdź odległość jaką przebędzie ciało od chwili t=0 do momentu, gdy prędkość ciała osiągnie wartość połowy wartości początkowej. Znajdź odległość jaką przebędzie ciało od chwili t=0 do zatrzymania się ciała.

Dane:
m
v₀
F = - kv
k - stała

Szukane:
s = ?

Wzory:
1. Przyspieszenie:

2. Prędkość:

3. II zasada dynamiki:

Rozwiązanie:
Uwaga!
Zadanie to jest bardzo trudne i jeśli nie wiesz co to znaczy pochodna i całka, nie zabieraj się za nie.

Zapiszmy równanie ruchu, wynikające z II zasady dynamiki

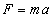Zauważmy, że siła zmienia się z każdą sekundą ruchu, bo zależy od prędkości. Popatrzmy na powyższy wzór. Skoro zmienia się siła, zmienia się przyspieszenie, bo masa ciała jest stała. Oznacza to, że nie możemy skorzystać z wzorów, które znamy, ponieważ słuszne były one tylko dla stałej wartości przyspieszenia. Skorzystajmy więc z bardziej ogólnej definicji przyspieszenia

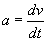Przyspieszenie to iloraz pochodnej prędkości po czasie. Podstawiamy to do naszego równania ruchu, oraz to, że F = -kv

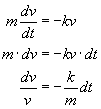Całkujemy z obu stron:

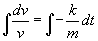Ponieważ wartości k i m nie zależą od czasu t to:

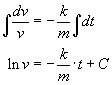gdzie C jest stałą całkowania.
Ponieważ w chwili początkowej, tzn. dla t = 0 prędkość v = v₀, to

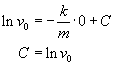Tak więc mamy

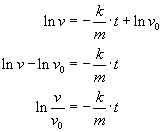co można przekształcić do postaci:

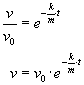
Mamy wzór na prędkość. Znajdziemy teraz drogę, jaką ciało przebędzie do chwili zatrzymania się.
Skorzystamy z definicji prędkości, ale tej ogólniejszej, która mówi że jest to pochodna drogi po czasie

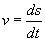Zatem:

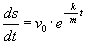Mnożymy obie strony przez dt i całkujemy

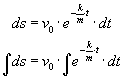Otrzymujemy

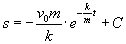gdzie C to stała całkowania.
Załóżmy, że dla t = 0, s = 0 i obliczamy stałą C

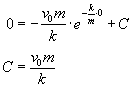Zatem zależność drogi od czasu ma postać:

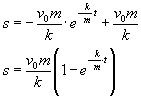Ciało zatrzyma się, gdy jego prędkość zmaleje do zera. Nastąpi to po nieskończenie długim czasie. Liczy to się w następujący sposób:

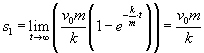s₁ to droga, jaką przebędzie ciało do chwili zatrzymania się.

Mamy jeszcze obliczyć odległość, jaką przebędzie ciało od chwili t = 0 do momentu, gdy prędkość ciała osiągnie wartość połowy wartości początkowej.
Obliczymy po jakim czasie t₂ prędkość ciała zmaleje do połowy. Powyżej podaliśmy wzór na prędkość:

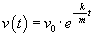Szukany czas obliczymy po rozwiązaniu równania

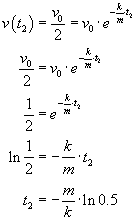Teraz korzystamy z wyliczonej wcześniej zależności drogi od czasu

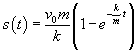Po czasie t₂ ciało, którego prędkość zmaleje do połowy przebędzie drogę

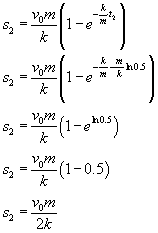Tak więc droga s₂ to droga, jaką przebędzie ciało od chwili t = 0 do momentu, gdy prędkość ciała osiągnie wartość połowy wartości początkowej.

Jamnik

« powrót do listy zadań

Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.

Teoria
Wyprowadzenia wzorów
Zadania fizyczne
Doświadczenia fizyczne
Tablice fizyczne
Biografie fizyków
FORUM
Oferty pracy

Zasady dynamiki Newtona

Zadanie ze statyki, mechaniki [0]
Zadanie ruch drgający [0]
Dlaczego opór w półprzewodnikach maleje do pewnej granicy, a potem wzrasta, ale minimalnie? [0]
Dlaczego ładunki elektryczne oddziałują na siebie? [0]
Zadanie o dyfrakcji światła pomocy [0]


	strona główna :: o serwisie :: polityka prywatności :: reklama :: mapa serwisu :: wstecz :: do góry