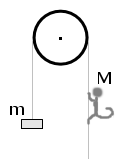
 Na linie przerzuconej przez blok nieruchomy i przyczepionej do ciężarka o masie m znajduje się małpa o masie M. Z jakim przyspieszeniem a będzie poruszać się ciężarek w następujących przypadkach:
a) małpa nie porusza się względem liny,
b) małpa wspina się po linie ze stałą prędkością v0 względem liny,
c) małpa wspina się po linie ze stałym przyspieszeniem a0 względem liny.
Przyjąć, że masy m i M poruszają się bez tarcia.
|
M
m
v0 (przypadek b)
a0 (przypadek c)
g
a = ? (dla każdego przypadku)
1. II zasada dynamiki:
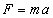
2. III zasada dynamiki
3. Siła ciężkości:
|
|
|
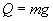
Rozrysujmy siły odgrywające jakąś rolę dla tego przypadku:
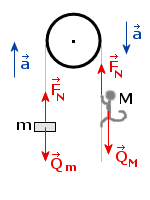Ponieważ zakładamy, że lina porusza się względem bloczku bez tarcia, to napięcie liny wszędzie musi być takie samo (III zasada dynamiki - patrz Zadanie 4). Czyli zarówno na małpę jak i na ciężarek działa taka sama siła FN skierowana w górę.
Przypadek a)
Małpa nie porusza się względem liny. Równania wynikające z II zasady dynamiki dla ciężarka i małpy mają postać:
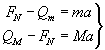Siłę ciężkości Q wyrażamy jako iloczyn masy oraz przyspieszenia ziemskiego:
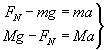gdzie a jest jednakowym przyspieszeniem zarówno dla ciężarka jak i małpy, skierowanym tak jak na rysunku. Dodając równania stronami, eliminujemy FN, otrzymując:
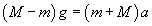a stąd przyspieszenie układu ciężarek-małpa wynosi:
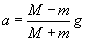Jeśli M > m to kierunek ruchu układu będzie zgodny z założonym na rysunku.
Przypadek b)
Jeżeli małpa porusza się względem liny ze stałą prędkością, to równania ruchu dla ciężarka i małpy są takie same jak w podpunkcie a) (stała prędkość nie ma wpływu na przyspieszenie). Czyli szukane przyspieszenie również wynosi:
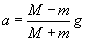Przypadek c)
Musimy teraz dokonać modyfikacji rysunku, ze względu na pojawienie się po stronie małpy przyspieszenia a0, skierowanego przeciwnie do przyspieszenia a:
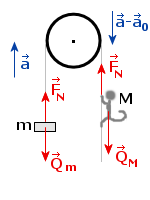Równania ruchu mają teraz, odpowiednio dla ciężarka i małpy, postać (siły ciężkości już rozpisano):
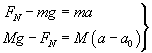gdzie teraz przyspieszenie małpy względem bloczka wynosi a - a0. Dodając oba równania stronami, otrzymamy:
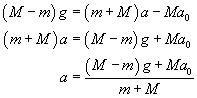
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
