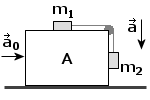
 Z jakim minimalnym przyspieszeniem powinien poruszać się klocek A, aby masy m1 i m2 pozostały w spoczynku względem niego? Współczynnik tarcia między klockiem i masami wynosi f = 0.2, natomiast m1=3kg a m2=5kg. Masę krążka i nici oraz tarcie w krążku zaniedbać.
|
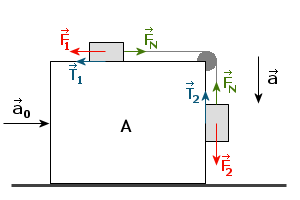Jeżeli klocek A porusza się w prawo z przyspieszeniem a0, to na masy m1 i m2 będą działać w lewo siły bezwładności m1a0 (siła F1) i m2a0. Siła m2a0 powoduje przyciskanie masy m2 do klocka powodując powstawanie siły tarcia T2 wyrażanej wzorem:
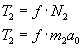gdzie N2 to siła nacisku masy drugiej na klocek A.
Siła tarcia T1 działająca na masę m1 wynika z siły ciężkości i wynosi:
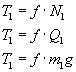Napiszmy teraz równanie ruchu wynikające z II zasady dynamiki dla masy m1 i m2 zakładając, że poruszają się one z pewnym przyspieszeniem a względem klocka, tak jak na rysunku.
Dla pierwszego ciała mamy:
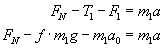oraz dla ciała drugiego:
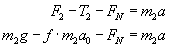gdzie FN jest siłą naprężenia nici łączącej obydwie masy (zgodnie z III zasadą dynamiki).
Z treści zadania wynika, że masy m1 i m2 mają pozostawać w spoczynku względem klocka A, tak więc ich przyspieszenie a musi równać się zeru. Zatem:
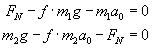Dodajmy te równania stronami:
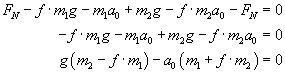I teraz łatwo możemy obliczyć przyspieszenie a0:
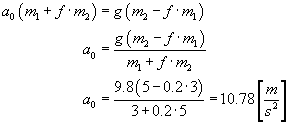Zatem minimalne przyspieszenie, z jakim powinien poruszać się klocek A, wynosi 10.78 m/s2.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
