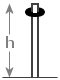 Po pionowym pręcie o wysokości h=5m zsuwa się pierścień (rysunek). Jeżeli praca sił tarcia pierścienia o pręt jest równa liczbowo 3/4 jego energii potencjalnej, to ile wynosi prędkość w chwili zderzenia pierścienia z podłożem?
|
Pierścień na wysokości h posiada energię potencjalną wyrażaną wzorem:
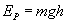Na pierścień działa siła ciężkości Q skierowana ku podłożu, oraz skierowana przeciwnie do niej siła tarcia. Działanie obu tych sił powoduje, że cała energia potencjalna zamieniana jest w pracę, gdy pierścień upadnie na ziemię, wtedy energia potencjalna będzie równa zeru, a wartość wykonanej pracy przez nasze dwie siły równa będzie wartości energii potencjalnej z wysokości h.
W zadaniu dane mamy, że 3/4 energii potencjalnej zamieniane jest na pracę sił tarcia. Wobec tego 1/4 energii potencjalnej zamieniana jest na pracę sił, które powodują opadanie. Oczywiście ciało nie spada z przyspieszeniem g, gdyż mamy tarcie, które spowalnia opadanie ciała. Tak więc załóżmy, że pierścień spada z jakimś stałym przyspieszeniem a (pod działaniem siły F), zatem porusza się ruchem jednostajnie przyspieszonym. Pierścień spadając, wykonuje pracę równą 1/4 energii potencjalnej:
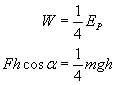Ponieważ kierunek i zwrot przesunięcia oraz siły F jest identyczny, zatem α = 0, a stąd cos 0 = 1. Siłę F możemy z II zasady dynamiki zapisać jako iloczyn masy i przyspieszenia, na koniec dzielimy otrzymany wzór przez h i przez m.
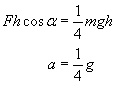Wzór się uprościł. Nie mamy przyspieszenia a. Korzystamy tak więc ze wzoru na przyspieszenie:
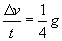Mamy do czynienia z ruchem jednostajnie przyspieszonym z prędkością początkową równą zeru, zatem (pojawia nam się szukana prędkość v):
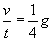Nie znamy jednak wartości czasu t. I co teraz? No właśnie, korzystamy z drugiego równania kinematycznego dla ruchu jednostajnie przyspieszonego, czyli z wzoru na drogę h (wysokość) w tym ruchu (wzór uprościłem, bo prędkość początkowa równa zeru):
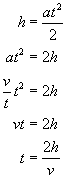Zauważcie, że pozbyłem się w przyspieszenia, a na koniec wyprowadziłem wzór na czas t.
No to teraz wstawiamy to do naszego równania i wyliczamy szukaną prędkość końcową ruchu v:
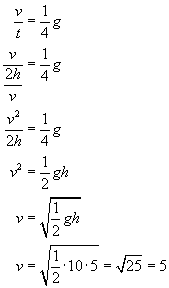Sprawdźmy jeszcze jednostkę:
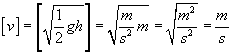Zatem pierścień uderzy o podłoże z prędkością 5 m/s.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
