Przyspieszenie na powierzchni pewnej planety będącej kulą o promieniu R wynosi g. Ile wynosi średnia gęstość tej planety?
|
Szukamy gęstości planety, skorzystać więc musimy z ogólnego wzoru na gęstość ciała
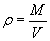
gdzie M to masa planety, a V - jej objętość.
Przyjmujemy, że nasza planeta jest kulą, korzystamy więc ze wzoru na objętość kuli:
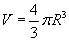
gdzie R to promień naszej planety. Wstawiamy ten wzór do wzoru na gęstość
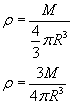
Nie jest nam znana niestety masa planety M, znamy jednak przyspieszenie grawitacyjne planety g. Dlaczego nie mielibyśmy skorzystać z prawa powszechnego ciążenia (siły grawitacji)? Załóżmy, że umieszczamy na powierzchni naszej planety jakieś ciało o masie m. Na takie ciało działa zarówno siła grawitacji FG i siła ciężkości Q:

A przecież te siły to nic innego jak... to samo :)
Zatem:
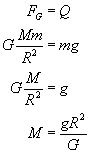
I w ten sposób mamy masę planety wyrażoną danymi - pamiętaj, że G to stała grawitacji, której wartość znajdziesz w każdych szanujących się tablicach fizycznych.
Wstawiamy naszą masę do wzoru na gęstość i otrzymujemy nasze rozwiązanie:
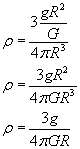
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
