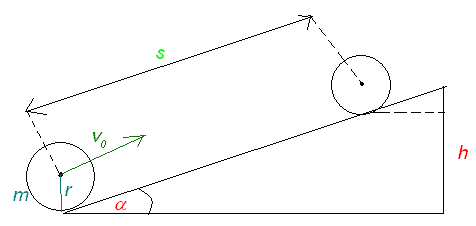
W górę równi pochyłej o kącie nachylenia α=30o wtacza się bez poślizgu kula, która u podstawy ma szybkość v0=10m/s. Oblicz drogę, jaką przebędzie wzdłuż równi do chwili zatrzymania się.
|
Aby rozwiązać to zadanie posłużymy się zasadą zachowania energii. W naszym przypadku przyjmie ona następującą postać:
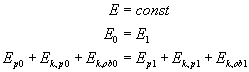
Przyjmijmy, że u podstawy równi energia potencjalna jest równa 0. Założenie to nie wpływa na wynik, ale uprości troche zapis. W tym samym momencie energia kinetyczna jest największa. Gdy kula się zatrzyma (na wysokości h) jego energia kinetyczna zmaleje do zera, a energia potencjalna osiągnie swoje maksimum. Uwzględniając te założenia możemy zasadę zachowania energii dalej przekształcać. Skorzystamy także z zależności między prędkością liniową i kątową oraz ze wzoru na moment bezwładności kuli (każdy chyba zauważy moment, w którym to zastosuję :) ).
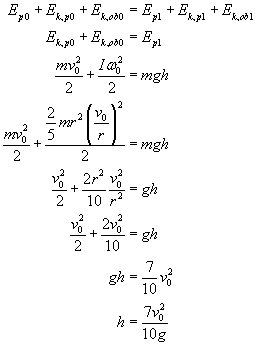
Zauważmy ponadto, że h/s=sinα. Możemy więc teraz policzyć drogę jaką przebędzie kula korzystając z wyniku poprzedniego przekształcenia i tej oczywistej zależności.
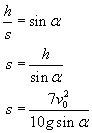
A teraz coś co wszyscy lubią, czyli sprawdzenie jednostek (czasami to pomaga wykryć jakiś błąd :)).
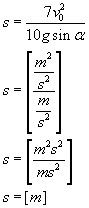
A na koniec policzymy wartość przebytej przez kulę drogi.
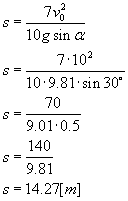
Szukana droga wynosi
s = 14.27 m.namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
