Odległość między okładkami kondensatora płaskiego o pojemności C zwiększono czterokrotnie, zmniejszając równocześnie trzykrotnie powierzchnię czynną okładek. Między okładki kondensatora wprowadzono dielektryk. Jaką powinien on mieć względną przenikalność elektryczną, aby pojemność kondensatora nie zmieniła się?
|
C
4 d1 = d2
S1 = 3 S2
εR = ?
1. Pojemność kondensatora
|
|
|
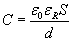
Pojemność kondensatora wyrażamy wzorem
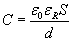gdzie:
d - odległość między okładkami,
S - powierzchnia czynna okładek,
ε0 - przenikalność elektryczna próżni (stała),
εR - przenikalność elektryczna środowiska (liczba niemianowana, w próżni jej wartość wynosi 1).
Policzymy najpierw pojemność kondensatora przed zmianami
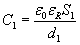Dla wygody zakładamy, że ów kondensator był próżniowy, zatem
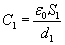Teraz dokonujemy zmian, rozsuwamy okładki, zmniejszamy ich powierzchnię i wsuwamy dielektryk
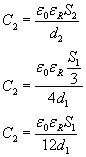Z treści zadania wiemy, że kondensatory mają ciągle tę samą pojemność
Podstawiamy pod pojemności to, co wyliczyliśmy wcześniej
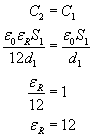Aby pojemność kondensatora nie zmieniła się, dielektryk powinien posiadać względną przenikalność elektryczną równą 12.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
