Fala poprzeczna rozchodząca się wzdłuż struny opisana jest równaniem
y=0.001sin(2000πt - 20πx)
gdzie x i y wyrażone są w metrach, czas t w sekundach. Ile wynosi okres drgań oraz długość fali? Ile wynosi prędkość rozchodzenia się tej fali?
|
Najpierw znajdziemy matematyczną formułę opisującą w ogólny sposób fale poprzeczne. Zauważmy, że struna wykonuje drgania w taki sam sposób jak fala płaska na wodzie. Przy wyprowadzaniu wzorów posłużymy się tym drugim przypadkiem. Wzór który wyprowadzimy będzie słuszny dla każdej fali tego typu.
Wyobraźmy sobie, że w gładką powierzchnię wody uderzamy płaską deseczką ze stałą częstotliwością ν. Przyjmijmy, że deseczka wykonuje ruch drgający. Wprawia ona wówczas w drgania harmoniczne cząstki wody znajdujące się w jej sąsiedztwie. Na skutek sił spójności drgania są przekazywane następnym cząstkom - po powierzchni wody rozchodzi się poprzeczna fala płaska. Drgania deseczki możemy opisać funkcją:
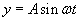
gdzie A jest amplitudą drgań, a ω częstością drgań.
Do punktu P odległego o x od źródła, czyli miejsca, w którym deseczka uderza o wodę, fala dotrze po czasie (porównaj poniższy wzór ze wzorem na drogę w ruchu jednostajnym prostoliniowym):
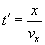
Drgania punktu P można więc opisać funkcją
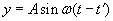
Łatwo odczytać, że wychylenie y punktu P osiągnie taką samą wartość jak wychylenie deseczki, jeśli od chwili rozpoczęcia mierzenia czasu upływa czas o t' dłuższy niż czas w wyrażeniu na wychylenie deseczki. Podstawiając wzór na t' do wzoru na wychylenie punktu P, otrzymujemy
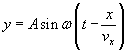
Pamiętajmy, że:
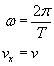
Ostatni fakt możemy zastosować, ponieważ współrzędna prędkości jest w tym przypadku równa wartości prędkości rozchodzenia się fali.
Możemy więc napisać:
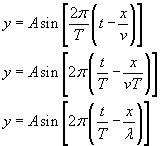
Zapiszmy teraz wzór z treści zadania tak aby przypominał powyższą funkcję.
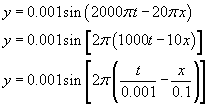
Porównajmy powyższy wzór z otrzymanym wcześniej równaniem fali (możemy tak uczynić, ponieważ fala na wodzie i drgania struny są opisane tą samą funkcją)
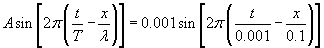
Z tego porównania natychmiast odczytujemy, że długość fali λ=0.1m, a okres fali T=0.001s. Teraz podstawiając odczytane wartości okresu i długości fali do wzoru na jej prędkość rozchodzenia się (porównaj z poprzednim zadaniem), mamy:
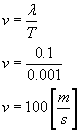
Okres fali wynosi 0.001 s, jej długość 0.1 m, a prędkość rozchodzenia się 100 m/s.namysłowianin
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
