Dwa klocki o masach mA i mB połączone nicią leżą na idealnie gładkiej powierzchni poziomej. Jaki warunek musi spełniać siła przyłożona do klocka B, aby nić nie zerwała się? Wiadomo, że nić wytrzymuje obciążenie FMAX.
|
mA
mB
FMAX
F = ?
1. II zasada dynamiki:
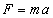
2. III zasada dynamiki
|
|
|
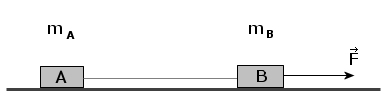Siła zewnętrzna F wywołuje przyspieszenie a obu klocków (dla obu klocków takie same). Ponieważ klocki te połączone są nicią, oddziałują na siebie wzajemnie, korzystamy więc z III zasady dynamiki. Spójrzmy na rysunek:
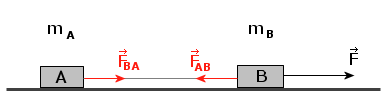Dorysowaliśmy na nim wektory sił wynikające z III zasady dynamiki, a co za tym idzie wartości tych wektorów są sobie równe (ale nie zwroty!). Na klocek B działa siła F i siła FAB, a na klocek A działa tylko siła FBA. Zgodnie z drugą zasadą dynamiki Newtona możemy napisać dwa równania, dla każdego klocka oddzielnie. Pamiętajmy, że zasada ta mówi, że siła po lewej stronie równania to siła wypadkowa.
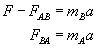Ponieważ jak pisaliśmy wyżej...
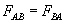...to siły te oznaczymy przez FN i nazwiemy je siłami naciągu nici, zatem:
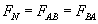Teraz możemy więc powyższy wzór zapisać jako:
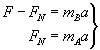Dodając stronami te równania eliminujemy FN. Otrzymujemy:
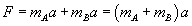Stąd obliczamy przyspieszenie:
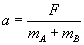A ponieważ...
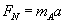...to...
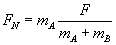...czyli otrzymujemy wzór na siłę naciągu nici dla naszego przypadku.
Nić zatem nie ulegnie zerwaniu, gdy siła naciągu nici będzie mniejsza od siły FMAX:
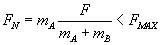Stąd otrzymujemy warunek na siłę F, przy którym nić nie ulega zerwaniu:
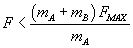
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
