fizyka.org :: fizyka.jamnika.pl :: mamy 15 lat!

Strona główna Teoria Zadania Wzory Forum SzukajFAQ O nas

Strona główna > Zadania z fizyki > Zasady dynamiki Newtona > Zadanie 9

Zasady dynamiki Newtona - Zadanie 9

Treść:
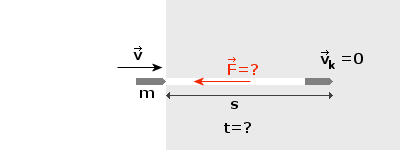
Pocisk o masie m=10g wystrzelony z pistoletu trafia w drewnianą belkę z szybkością v=300m/s i wbija się na głębokość s=5cm. Obliczyć:
a) wartość siły działającej na pocisk,
b) czas hamowania pocisku w belce.
Przyjąć, że ruch pocisku jest jednostajnie opóźniony.

Dane:
m = 10 g = 0.01 kg
v = 300 m/s
s = 5 cm = 0.05 m

Szukane:
F = ?
t = ?

Wzory:
1. II zasada dynamiki:

2. Wzór na przyspieszenie:

3. Droga w ruchu jednostajnym opóźnionym:

Rysunek:

Rozwiązanie:
W zadaniu mamy policzyć czas hamowania t oraz wartość siły hamującej F. Siłę wyliczamy korzystając z II zasady dynamiki:

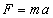Spójrzmy na dane, hm... nie mamy przyspieszenia. Trzeba więc odwołać się do wzoru na przyspieszenie:

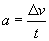Mamy tu do czynienia z ruchem jednostajnym opóźnionym, tak więc Δv to różnica prędkości początkowej i końcowej, a ponieważ u nas prędkość końcowa równa jest zeru, to Δv = v, zatem:

Wyprowadziliśmy od razu wzór na czas, ponieważ również mamy go wyliczyć. No tak, ale nic to nam nie dało. Musimy więc skorzystać z drugiego równania kinematycznego dla ruchu opóźnionego, czyli z wzoru na drogę (oznaczyliśmy prędkość początkową przez v):

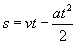Podstawmy za t wyliczoną przez nas powyżej wartość:

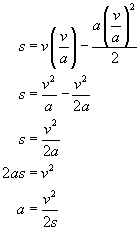Teraz możemy w końcu wyliczyć naszą siłę:

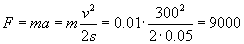
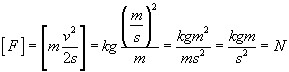Jak widać, jednostka się zgadza, obliczmy więc teraz czas:

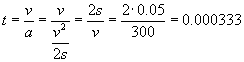
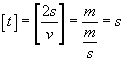Dla czasu wyszła sekunda, co oznacza, że koniec zadania.

Wartość działającej siły na pocisk wynosi 9000 N, a czas jego hamowania wynosi około 0.000333 s.

Jamnik

« powrót do listy zadań

Znalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.

Teoria
Wyprowadzenia wzorów
Zadania fizyczne
Doświadczenia fizyczne
Tablice fizyczne
Biografie fizyków
FORUM

Zasady dynamiki Newtona
Ruch jednostajnie opóźniony

Zadanie [0]
Miernictwo [0]
Miernictwo [0]
Miernictwo [0]
SPRAWOZDANIE (moc?) [1]

Serwis "Fizyka Jamnika" używa plików cookies. Są to pliki instalowane w urządzeniach końcowych osób korzystających z serwisu, w celu administrowania serwisem, poprawy jakości świadczonych usług w tym dostosowania treści serwisu do preferencji użytkownika, utrzymania sesji użytkownika oraz dla celów statystycznych i targetowania behawioralnego reklamy (dostosowania treści reklamy do Twoich indywidualnych potrzeb). Informujemy, że istnieje możliwość określenia przez użytkownika serwisu warunków przechowywania lub uzyskiwania dostępu do informacji zawartych w plikach cookies za pomocą ustawień przeglądarki lub konfiguracji usługi. Szczegółowe informacje na ten temat dostępne są u producenta przeglądarki, u dostawcy usługi dostępu do Internetu oraz w Polityce prywatności.


	strona główna :: o serwisie :: polityka prywatności :: reklama :: mapa serwisu :: wstecz :: do góry