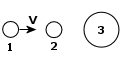 Rysunek przedstawia układ trzech kulek. Kulki 2 i 3 spoczywają. Jeżeli zderzenie 1 i 2 kulki jest doskonale sprężyste centralne, to ile będzie wynosiła prędkość w wyniku zderzenia centralnego niesprężystego kulek 2 i 3?
|
m1 = m
m2 = m
m3 = 3m
v1 = v
u23 = ?
1. Zderzenia ciał
2. Zasada zachowania pędu
3. Zasada zachowania energii
4. Pęd:
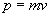
5. Energia kinetyczna:
|
|
|
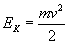
Zadanie rozwiążemy w dwóch etapach.
[Zderzenie sprężyste kulek 1 i 2]
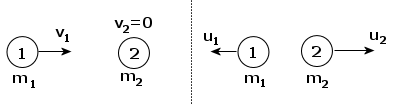W zderzeniach sprężystych możemy korzystać zarówno z zasady zachowania pędu, jak i z zasady zachowania energii. Zajmiemy najpierw się tą pierwszą.
Pęd kulek przed zderzeniem:
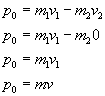Ponieważ kulka druga jest w spoczynku, wzór nam się redukuje. W ostatnim kroku podstawiliśmy wartości z zadania.
Znajdźmy teraz pęd kulek po zderzeniu:
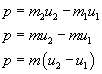Korzystamy teraz z zasady zachowania pędu:
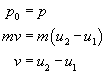Interesuje nas wyliczenie prędkości u2, gdyż będzie ona nam potrzebna w następnym etapie.
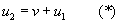Mamy jednak dwie niewiadome - u1 i u2. Skorzystamy z zasady zachowania energii. Energią jest w tym przypadku suma energii kinetycznych kulek. Energia kinetyczna kulek przed zderzeniem jest równa:
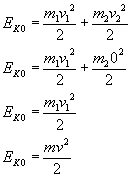Podobnie, jak powyżej, prędkość v2 jest równa zeru i wzór redukuje się do prostszej postaci. Na koniec podstawiliśmy dane z zadania.
Teraz szukamy energii kinetycznej kulek po zderzeniu:
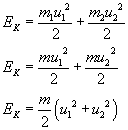Czas na skorzystanie z zasady zachowania energii:
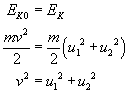Do tego wzoru podstawiamy (*):
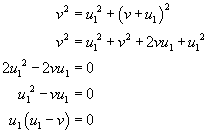Równanie ma wtedy rozwiązanie, gdy:
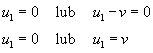Kula 1 nie może mieć po zderzeniu prędkości v, gdyż ją posiadała przed zderzeniem, a po zderzeniu musiała oddać część pędu i energii kuli drugiej. Stąd:
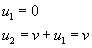Zatem kula druga mknie do kulki 3 z prędkością v.
Możemy zapamiętać, że w zderzeniach sprężystych, jeżeli dwie kule zderzają się, a jedna z nich jest przed zderzeniem w spoczynku, to po zderzeniu kula uderzająca zatrzymuje się i przekazuje cały pęd i całą energię kuli drugiej. Tak jest zawsze.
[Zderzenie niesprężyste kulek 2 i 3]
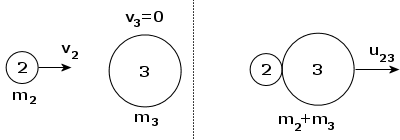W zderzeniach niesprężystych możemy korzystać tylko z zasady zachowania pędu. Przyjmujemy zgodnie z powyższym, że v2 = u2
Pęd przed zderzeniem:
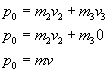Ten przypadek niczym się nie różnił od poprzedniego.
Pęd po zderzeniu (pamiętaj, że w tym typie zderzeń kulki poruszają się razem):
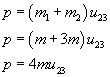Wykorzystujemy zasadę zachowania pędu:
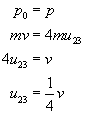Po mozolnych obliczeniach otrzymaliśmy wynik. Prędkość kulek 2 i 3 po zderzeniu niesprężystym jest równa jednej czwartej prędkości początkowej kulki 1.
Uwaga! Zderzenie centralne oznacza to, że kulki uderzają się tak, że poruszają się potem po tej samej prostej.
Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
