Aby wyliczyć pojemność C kondensatora, skorzystamy z naszej wiedzy dotyczącej elektrostatyki, a dokładnie z zagadnienia dotyczącego strumienia natężenia pola elektrycznego.
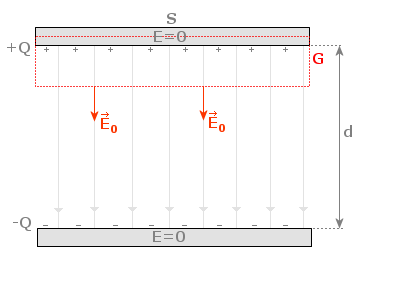Na podstawie prawa Gaussa wyznaczamy natężenie pola E0 wewnątrz kondensatora próżniowego. Ze względu na symetrię wybieramy powierzchnię Gaussa G (linia przerywana na rysunku) w kształcie prostopadłościanu o jakiejś wysokości h (mniejszej od d) i podstawie równej powierzchni okładki kondensatora S. Strumień wektora E0 przechodzący przez górną ścianę prostopadłościanu, która leży wewnątrz płytki jest równy zeru, ponieważ wewnątrz naelektryzowanego przewodnika E = 0 (zobacz temat "Pole elektrostatyczne przewodnika kulistego" w Wyprowadzeniach). Strumień przechodzący przez boczne ściany, również jest równy zeru, gdyż linie sił pola ślizgają się po tych powierzchniach. Wobec tego całkowity strumień Φ przechodzący przez wybraną powierzchnię Gaussa jest równy strumieniowi przechodzącemu przez podstawę prostopadłościanu leżącą między okładkami kondensatora, zatem
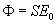Wewnątrz powierzchni Gaussa znajduje się ładunek +Q zgromadzony na powierzchni okładki kondensatora. Z prawa Gaussa całkowity strumień wektora E przechodzący przez zamkniętą powierzchnię Gaussa wynosi:
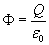Porównujemy oba wyrażenia
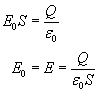Jeżeli nasz kondensator wypełniony jest dielektrykiem o stałej dielektrycznej εR, to natężenie pola w kondensatorze jest εR mniejsze:
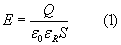Natężenie E jednorodnego pola elektrycznego wewnątrz naładowanego do napięcia U kondensatora jest równe (patrz rozdział "Kondensator - natężenie pola" w Wyprowadzeniach):
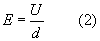Porównując (1) z (2) otrzymujemy:
Ponieważ iloraz Q / U jest pojemnością elektryczną C, to
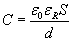« powrót do listy wyprowadzeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
