Rozpatrujemy gaz znajdujący się w naczyniu, które ma kształt sześcianu o krawędzi l. W naczyniu tym jest N cząsteczek, przy czym należy podkreślić, że N jest dużą liczbą. Jeżeli np. dysponowalibyśmy jednym molem gazu, liczba cząsteczek wynosiłaby
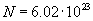Cząsteczki poruszają się we wszystkich możliwych kierunkach, co oznacza, że statystycznie jednym z trzech zasadniczych kierunków (x, y, z) porusza się N/3 cząsteczek. Poruszające się cząsteczki zderzają się ze ścianami naczynia i wywierają w zbiorniku pewne ciśnienie.
Rozpatrzmy wybraną (statystyczną) cząsteczkę o średnich parametrach: prędkości v i tym samym średniej energii kinetycznej EK.
A. Obliczenie F1 - siły działania jednej cząsteczki na ścianę podczas zderzenia się jej z tą ścianą.
Pęd cząsteczki przed zderzeniem...
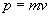...i po zderzeniu:
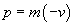Podczas zderzenia cząsteczka zmienia swój pęd o:
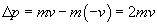Z uogólnionej zasady II dynamiki (popęd siły równy jest przyrostowi pędu):
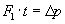Uwzględniając obliczony przyrost pędu cząsteczki, otrzymamy:
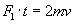Czas t jest czasem, w którym zachodzi rozpatrywana zmiana pędu. W czasie tym cząsteczka przebędzie drogę 2l, tj. od ściany do przeciwległej ściany i z powrotem, by ponownie zderzyć się z daną ścianą, a tym samym zmienić swój pęd.
Z równania drogi w ruchu jednostajnym prostoliniowym (mamy do czynienia z gazem doskonałym):
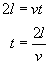Podstawiamy powyższe do wzoru na szukaną siłę:
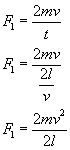Zauważmy, że energia kinetyczna wynosi...
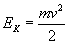...a więc nasza siła:
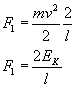
B. Obliczenie F - siły działania N/3 cząsteczek na ścianę podczas zderzenia z tą ścianą.
Powyżej opisaliśmy sytuację dla jednej cząsteczki, teraz mamy ich N/3, tak więc:
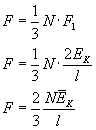gdzie EK to średnia energia kinetyczna cząsteczek, wzór której wyprowadzam w innym miejscu (patrz dział "Wyprowadzenia wzorów"). Dla zaznaczenia "średniości" tej energii użyliśmy daszka.
C. Obliczenie ciśnienia p wywieranego przez gaz w zbiorniku.
Z definicji ciśnienia:
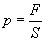Ciśnienie to jest wywierane identycznie na każdą ze ścian naczynia w kształcie sześcianu, dla którego powierzchnia jednej ściany wynosi:
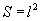Na podstawie tego możemy wyliczyć ciśnienie wywierane przez gaz w zbiorniku (a właściwie na jedną ścianę przez 1/3 cząsteczek w nią uderzających:
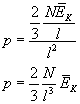Ponieważ l3 to objętość V naczynia, więc
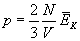
Ciśnienie gazu w zbiorniku zamkniętym jest wprost proporcjonalne do liczby cząsteczek w naczyniu i średniej energii kinetycznej cząsteczek, a odwrotnie proporcjonalne do objętości naczynia.
Zauważcie, że ciśnienie gazu nie zależy od kształtu naczynia.« powrót do listy wyprowadzeńZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
