Z jakim przyspieszeniem będzie się zsuwać z równi pochyłej ciało, jeżeli kąt nachylenia α=30o, a tarcie pomijamy? Jaką szybkość końcową osiągnie ciało zsuwające się z wysokości h=2m?
|
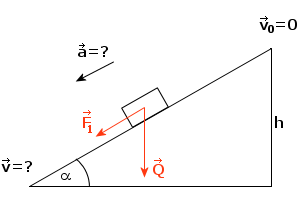Policzmy najpierw przyspieszenie, jakie osiąga nasze ciało. Przed rozwiązaniem tego zadania należy przeczytać temat o równi pochyłej z wyprowadzeń wzorów (link znajduje się po prawo). Dowiecie się stamtąd, że skoro tarcia nie ma, to jedyną siłą odgrywającą rolę w ruchu jest siła F1, którą wyrażamy wzorem:
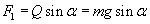Zatem korzystamy z II zasady dynamiki i otrzymujemy natychmiast wzór na przyspieszenie:
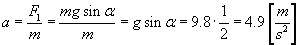
Policzmy teraz szukaną prędkość końcową. Prędkość takową możemy obliczyć, korzystając ze wzoru na przyspieszenie (Δv = v, ponieważ v0 = 0):
Nie mamy jednak danego czasu ruchu. W takim przypadku korzystamy z drugiego wzoru charakterystycznego dla ruchu jednostajnego prostoliniowego (wzór został uproszczony, ponieważ v0 = 0):
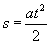Wyliczamy z tego wzoru czas:
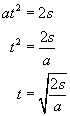Ale zaraz! Nie mamy jeszcze drogi s. Mamy jednak wysokość równi h oraz jej kąt nachylenia α. Tak więc:
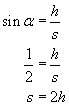Teraz to wszystko możemy złożyć...
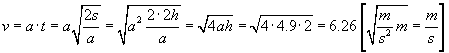Otrzymaliśmy prędkość i prawidłową jednostkę.
Ciało porusza się z przyspieszeniem równym 4.9 m/s2, a na końcu swej drogi osiąga prędkość 6.26 m/s.Jamnik
« powrót do listy zadańZnalazłeś błąd w materiale? Skontaktuj się z nami, przysyłając adres strony, na której znajduje się błąd i informację o tym, czego dotyczy błąd.
